


실 물체(Real objects)들은 언제나 렌즈의 앞쪽에 있고 허 물체(virtual objects)들은 언제나 렌즈의 뒤쪽에 있다. 허 물체는 광학계 내에 있는 어떤 광학소자들에 의하여 만들어진다. 실상들은 언제나 렌즈 뒤쪽에 형성되며, 허상들은 렌즈의 앞쪽에 있게 된다. 여기서는 렌즈에 의한 상 형성에 대하여 다루는데 상공간과 물체공간사이를 구분하는 것은 중요하다.
물체와 상이 렌 즈의 앞과 뒤 등 어디에 있든지 간에 그들은 각각 물체 공간과 상 공간에 속 한다 따라서 물체공간과 상 공간들은 둘 다 士 무한대까지 확장된다. 굴절하기 전에는 빛이 물체공간에서 이동하지만 굴절 후에는 상 공간에서 이동한다.
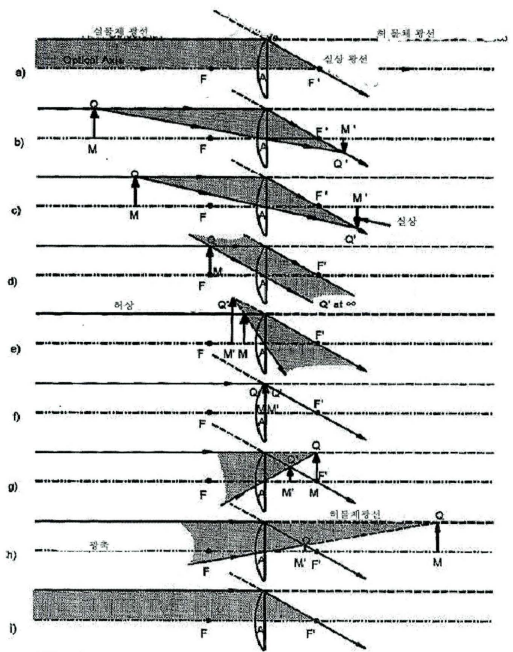
- 물체가 - 무한대 에 있으면 상은 F’에 있는 점이 된다.(a)
- 실 물체 MQ처럼 F로 향해 접근하면 도립실상 M'Q’가 만들어지는데+ 무한대로 향해 이동하면 M'Q’는 점점 커지며, 상의 위치는 + 무한대로 향한다. (b, c)
- 실 물체가 F로부터 A로 계속접근해가면 축소된 정립허상이 만들어지는데 상은 ― OO로부터 A 로 이동한다.(d, e)
- 물체가 렌즈에 도달하면 상은 동시 적으로 렌즈에 도달하며 A 에서 부합된다.(f)
- 물체가 A와 + 무한대 사이 의 영역에 있으려면 물체는 허물체이여야 한다. 그러면 상은 A로부터 F'로 이동한다. 이때 상은 정립싣상이고 물체보다 작다.(g,i)
이 볼록렌즈 의 경우를 요약하면, 여기서 RO = 실물체, RI= 실상, VO = 허물체이고 VI = 허상 이다.
이제 이를 표로 정리해보자.
| 물체 위치의 이동 | 상 위치의 이동 | 상의 특성 |
| -무한대로부터 F | F로부터 +무한대 | RO/RI 도립상 |
| F로부터 A | -무한대로부터 A | RO/VI 정립상 |
| A로 부터 +무한대 | A로 부터 F | VO/RI 정립상 |
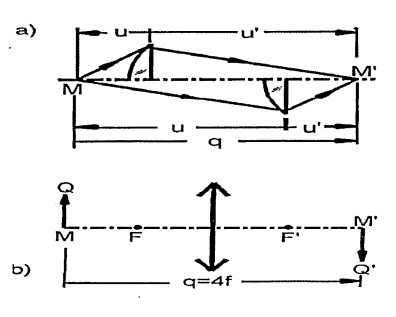
간격 \( q = MM' = -u + u' \) 또는 \( u' = u + q \)이다. 이 값을 얇은 렌즈 공식에 대입하여 \( u \)에 대하여 풀면
\[ \frac{1}{u'} = \frac{1}{u} + \frac{1}{f} \]
\[ u = -q \pm \sqrt{q(q - 4f)} / 2 \]
만일 이차방정식에서 두 개의 실수해를 구하려한다면 \( (q - 4f) \) 항이 0보다 크거나 같아야 한다.
\( (q - 4f) \) 항이 0보다 크다는 것은 물체와 상 사이의 간격이 동일한 결과를 나타내는 물체거리가 두 개 있음을 의미한다(a).
최소간격은 \( (q - 4f) = 0 \)일 때 발생한다. 그러면 \( u = -2f, u' = 2f \)이고 측 배율은 -1로서 같다.
'Optics > Ray optics' 카테고리의 다른 글
| 42. 얇은 렌즈의 초점면과 초점 상 (1) | 2023.12.01 |
|---|---|
| 41. Newtonian 방정식 (2) (1) | 2023.11.30 |
| 39. 비축상점의 작도법과 측(횡) 배율 (1) | 2023.11.30 |
| 38. 초점 거리 (0) | 2023.11.29 |
| 37. 렌즈 공식 중간 정리 (0) | 2023.11.29 |



