

42. 얇은 렌즈의 초점면과 초점 상Optics/Ray optics2023. 12. 1. 22:32
Table of Contents
반응형

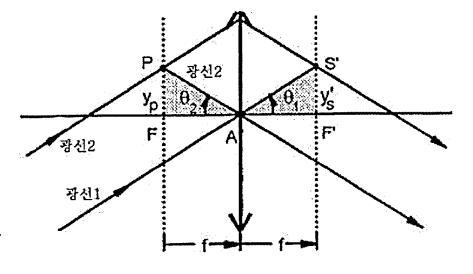
초점은 초점면이라 불리는 횡 평면 위에 있다.
그림을 참고하면, F를 관통하는 제 1 또는 1차 초점면은 무한에서 공액상을 갖는다.
무한 물체 면은 F'에 있는 제 2 초점면에 대하여 공액이다.
무한히 먼 비축물체 S는 렌즈 쪽으로 시준된 광선(평행광선)을 보내게 된다.
제2초점면에서 상 S'의 높이 (또는 크기)를 결정하기 위하여 중심 A를 통과하는 광선1을 입사 시킨다.
이 광선은 S'에 있는 제2초점면과 교차된다. 광선1에 평행한 광선2는 제1초점면에 있는 P점과 교차된다.
광선 2는 물체 S에서 나왔으므로 이 광선은 또한 S를 통과하도록 굴절되게 된다.
상의 크기 y's = F'S'이다. 광선 기울기 = 0이다
삼각형 AF'S'에 의하여
\( \tan \theta_1 = \frac{F'S'}{AF'} = \frac{y's}{f} \) 또는 \( y's = f \tan \theta_1 \)
각이 작을 경우에는 \( y's = f \theta_1 \)
P 점은 렌즈의 제1초점면에 있는 비축 물체를 나타낸다.
P 점으로부터의 광선은 렌즈에 의하여 수렴되어 무한에 상P'가 형성된다.
주광선(광선3)의 기울기 θ_2는 물체공간과 상 공간에서 일정하다. 삼각형 PFA에서 물체높이 yp = FP이다.
\( \tan \theta_2 = \frac{FP}{AF} = \frac{yp'}{f} \) 또는 \( yp = f' \tan \theta_2 \)
반응형
'Optics > Ray optics' 카테고리의 다른 글
| 44. 광선 수차란 무엇인가? (1) | 2023.12.22 |
|---|---|
| 43. 렌즈계의 Stop과 Pupil들 (1) | 2023.12.01 |
| 41. Newtonian 방정식 (2) (1) | 2023.11.30 |
| 40. 얇은 렌즈에 의한 상의 형성 (0) | 2023.11.30 |
| 39. 비축상점의 작도법과 측(횡) 배율 (1) | 2023.11.30 |



