


기하광학에서는 주어진 물체 점에서 나온 모든 광선이 대응되는 상점으로 정확하게 이동하는 완전광학계를 다루었다.
아래 그림에 있는 결상 광학 계를 보면 물체를 떠난 여러 광선들 중에서 일부의 광선들을 보여주는데 궁극적으로는 일부의 광선들만이 상에 도달하고 있음을 보여준다
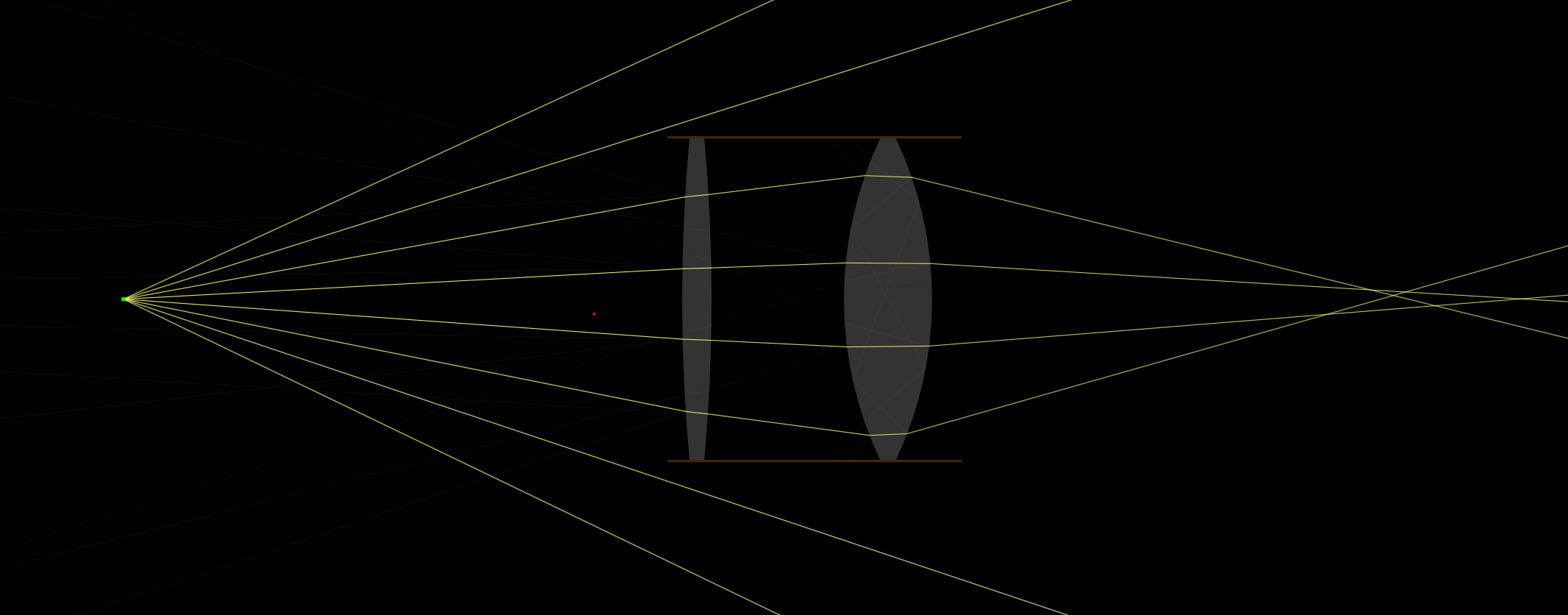
실제 광학계는 다음의 세 가지 중요한 이유 때문에 완전하다고 할 수 없다.
(i) 물체를 떠난 광선 중의 일부는 광학계에 결코 들어갈 수가 없다. 빛의 파동 적 성질에 의해 회절이 발생하게 되고 일부 광선들을 잃어버리게 되어 결 과적으로 상이 흐려지게(blurring)된다.
(ii) 광학계에 들어간 광선들 중의 일부도 굴절과 난반사, 규칙반사, 흡수 등에 의해 손실 되어 상을 형성하는데 기여하지 못한다.
(iii) 또한 물체 점을 출발하여 광학계를 통과한 광선들이 정확히 반사의 법칙 과 굴절의 법칙을 따랐다고 해도 하나의 상점에 모두 다 도달하지는 못 한다. 이런 제한 요인들(한 점으로 가지 못하는)을 광선수차(Ray Aberration)라 부른다.
앞에서는 근축 근사를 사용하였고,
또한 곡면 표면에서의 굴절과 반사만 고려하였기 때문에 완전 결상으로 기술할 수 있었다.
근축광선을 가정하는 근축이론은 광학계에서 완전한 상을 만들게 한다.
이때는 물체의 각 점으로부터 나온 모든 광선들은 상의 공액점에서 만난다.
이 경우 상 은 아마도 크기를 제외하고는 물체의 정확한 복사본이다.
그러나 근축광선은 대부분의 실제 광학계에서는 굴절되거나 반사된 모든 광선 들 중의 아주 작은 부분에 지나지 않는다.
그러므로 실제의 경우에는 근축상도 물체와 동일한 완전한 나타내지는 못한다.
광축 위에 있는 물체 점으로부터의 광선들 중 광축에 대하여,
증가된 각으로 또는 사각으로 물체로부터 나온 광선들은 수차를 갖게 된다.
이런 광선들은 근축광선들처럼 상평면에 있는 동일한 한 점에서 교차되지 않게 되고,
결과적으로 번지거나 왜곡된 상이 만들어진다.

위 그림에서는 광축 위에 있는 광선과 렌즈의 전체개구를 가로질러 입사하는 비축 정집(tangential) 연필광선을 보여준다. 정점(tangential)광선들은 광축이 포함된 자오선의(meridional)평면에 놓여 있다.
개구의 모서리부분에 있는 임의 연필광선들은 가장자리(marginal)광선이라 부른다.
이것은 개구의 둘레에 있는 여러 광선들에 의해 구성 되는 광선 고리중의 하나이다.
축과 가장자리사이에서 어떤 높이로 렌즈에 입사되는 광선들을 띠 모양 광선(zonal ray)들이라 한다.
띠 모양 광선들은 렌즈개구의 높이에 대한 비율을 사용 하 여 분수 값으로 나타낸다.
한 예로 개구 전체의 0.7 또는 0.5로 쓴다. 개구의 중심을 지나 진행하는 주광선은 물체의 각 점으로부터 출발한 연필광선들에 둘러 쌓여있다.

이번 위 그림에 보여지는 sagittal면은 자오선면에 수직이다.
sagittal연필 광들은 또한 띠 모양 광선들과 가장자리 광선들에 둘러 쌓여있다.
광축이 포함된 평면 내에 놓여있지 않은 광선들을 skew rays라 부른다.
'Optics > Ray optics' 카테고리의 다른 글
| 46. 광학 수차의 비교 (0) | 2023.12.22 |
|---|---|
| 45. 색 수차와 단색 광학 수차 (1) | 2023.12.22 |
| 43. 렌즈계의 Stop과 Pupil들 (1) | 2023.12.01 |
| 42. 얇은 렌즈의 초점면과 초점 상 (1) | 2023.12.01 |
| 41. Newtonian 방정식 (2) (1) | 2023.11.30 |



