


색 수차와 단색 광학 수차
광학 시스템의 완성 단계에서 이미지 생성 시 불완전한 광선이 휘어지는 현상에 의해 제품에 발생하는 빛의 굴곡. 모든 광학 시스템에서 수차는 필연적으로 존재한다.
가장 일반적인 수차의 종류로는 색수차, 구면수차, 비대칭수차(coma), 비점수차(astigmatism), 상면 만곡(field curvature) 및 왜곡이 있다.
광학 시스템을 설계하는 작업은 결코 만만한 일이 아니다.
즉 완벽한 디자인의 시스템이라도 광학 수차는 존재하기 마련이다.
최적의 시스템을 생성하기 위한 최고의 방법은 광학 수차를 제대로 이해하고 보정하는 것이다.
이를 위해서는 우선 광학 시스템에 존재하는 광학 수차의 유형을 검토해야 한다.
광학 수차는 완벽한 수학적 모델과의 편차를 의미한다. 이러한 편차는 물리적, 광학적 혹은 수학적 결함이 원인이 아니라는 점을 유의해야 하고.. 오히려 렌즈 자체의 형태, 빛의 파동 특성 또는 시스템 내에서의 광학 요소 배치로 인해 발생할 가능성이 있다.
광학 시스템은 이미지의 크기와 위치를 구하기 위해 일반적으로 1차 혹은 근축 광학을 이용하여 설계된다.
근축 광학의 경우에는 광학 수차를 고려하지 않는다. 이는 광선을 빛으로 취급함에 따라 수차를 유발하는 파동 현상은 제외시키기 때문이다.
광학 수차의 이름과 특성은 다양한 방식으로 지정된다. 수차를 단순하게 두 그룹으로 분류하자면, 색 수차(두 개 이상의 파장광을 사용할 때 나타남)와 단색 수차(단일 파장광을 사용할 때 나타남)로 나뉠 수 있다.
색 수차
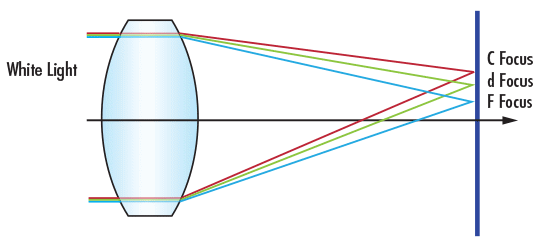
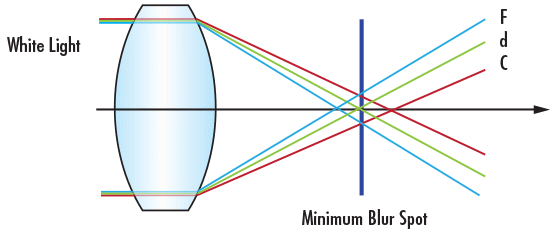
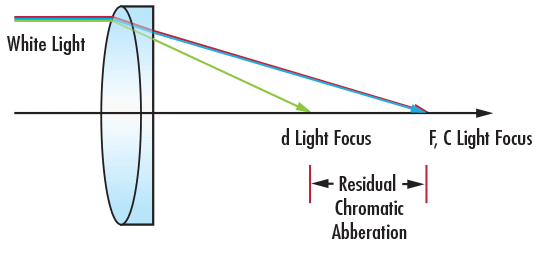
색 수차(Chromatic aberration)는 더 나아가 횡방향과 종방향의 두 가지 유형으로 분류된다.
종방향은 1차 혹은 2차 종방향 색수차로 다시 구분될 수 있다.
횡방향 색수차(TCA: Transverse Chromatic Aberration)는 이미지의 크기가 파장에 따라 변화할 때 발생한다.
다시 말해 백색광을 사용하면 적색, 황색 및 청색 파장은 수직면에서 개별 지점에 초점을 맞춘다.
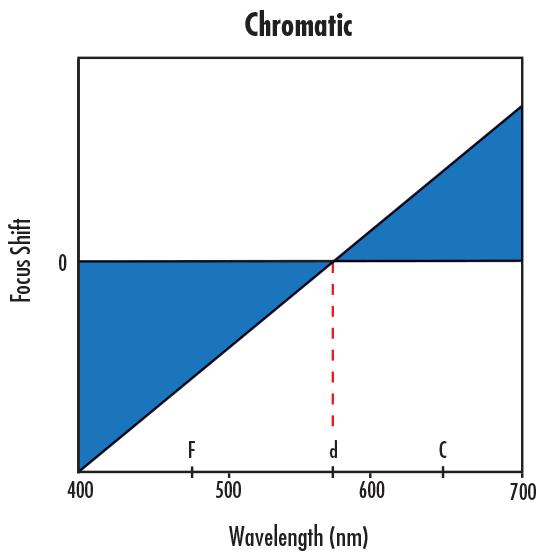
광학 용어에서 656.3nm (적색)는 C 라이트, 587.6nm (황색)는 d 라이트, 그리고 486.1nm (청색)는 F 라이트로 간주한다.
이러한 명칭은 C & F 라이트에 대한 수소 방출 라인과 d 라이트에 대한 헬륨에서 비롯된다.
종방향 색수차(LCA: Longitudinal Chromatic Aberration)는 유리의 분산 특성의 결과로 서로 다른 파장이 수평 광학 축을 따라 다른 지점에서 초점을 맺을 때 발생한다. 유리의 굴절률은 파장에 따라 다르기 때문에 파장광이 초점을 맞추는 위치에 따라 미치는 영향력이 약간씩 차이가 있음으로써 수평면을 따라 F, d 및 C 라이트는 별도의 초점(focal point)을 갖게 된다.
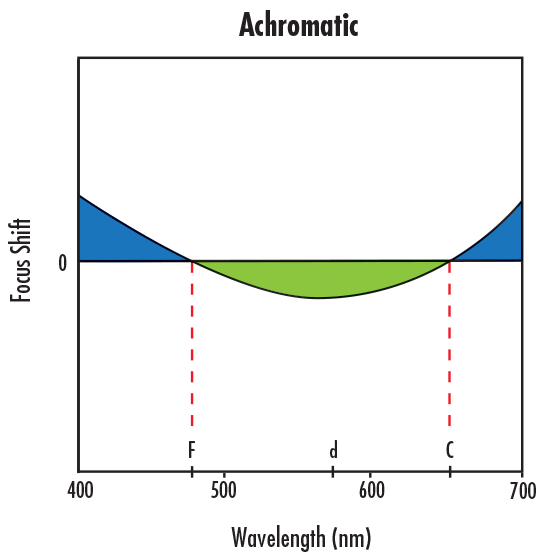
1차 종방향 색수차의 보정은 일반적으로 굴절률이 다른 positive lens와 negative lens 요소로 구성된achromatic doublet lens를 사용한다.
이러한 유형의 보정은 동일한 위치에 F와 C 라이트의 초점이 맺히도록 하지만 잔류 색수차를 유발하는 d 라이트 초점의 위치에는 거의 영향을 미치지 않기 때문이다.
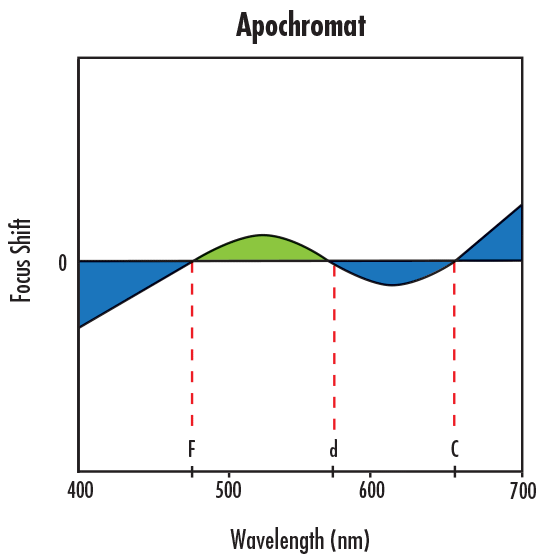
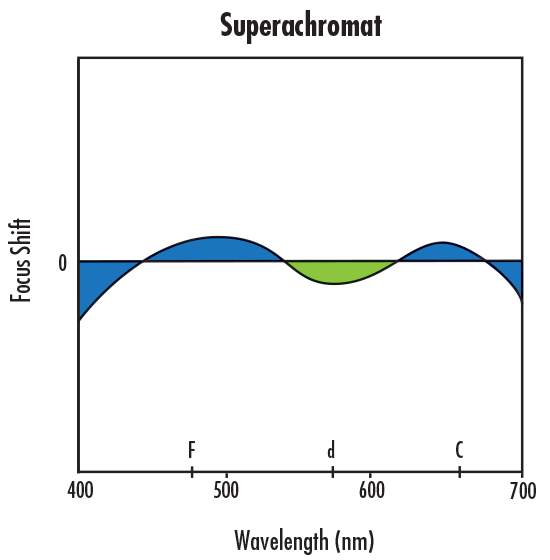
잔류하는 종방향 색수차를 보정하기 위해서는 더욱 복잡한 렌즈나 렌즈 시스템을 이용해야만 빛의 초점을 이동시켜가며 F와 C 포커스와 동일한 축에 위치시킬 수 있다. 이와 같은 보정을 위해서는 동일한 지점에서 3개 파장의 초점을 맞추는 apochromatic lens를 사용하거나 동일한 지점에서 4개 파장의 초점을 맞추는 superachromatic lens를 사용하면 된다.
단색 수차
단색 수차(Monochromatic aberration)는 색 수차에 비해 훨씬 더 많은 유형으로 존재한다. 이에 따라 단색 수차에는 명칭 뿐만 아니라 웨이브프런트 계수도 함께 표시해야 한다. 예를 들어 구면 수차의 웨이브프런트 계수는 040이다. 이러한 웨이브프런트 계수는 완벽한 웨이브프런트와 수차가 있는 웨이브프런트 사이의 실제 차이를 알려주는 수학적 합계로 구해진다.
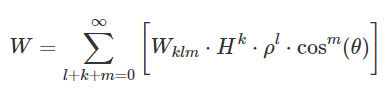
공식 1에서 은 웨이브프런트 계수, 는 정상화된 이미지의 높이, 는 동공의 위치, 그리고 는 두 벡터의 외적에 따라 도달할 경우 두 벡터 사이의 각도를 의미한다.
일단 웨이브프런트 계수를 알고 있다면 I와 를 추가해 차수(order number)를 구할 수 있다.
그러나 이러한 방식은 항상 짝수를 만들어 냅니다. 광학 차수는 대개 1차, 3차, 5차 등으로 칭해지기 때문이 일 경우에는 1차 수차가 되고 일 경우에는 3차 수차가 된다.
일반적으로 시스템 분석에는 1차와 3차 수차만 필요하다. 더 높은 차수의 수차가 존재하긴 하지만 시스템이 복잡해지기 때문에 고수차의 광학 시스템은 일반적으로 보정을 하지 않는다.
고차수의 수차를 보정하는 복잡한 보정 작업이 이미지 품질 개선에 도움이 되지는 않기 때문이다..
'Optics > Ray optics' 카테고리의 다른 글
| 47. 단색수차, 그리고 3차 이론과 구면수차 (1) | 2023.12.22 |
|---|---|
| 46. 광학 수차의 비교 (0) | 2023.12.22 |
| 44. 광선 수차란 무엇인가? (1) | 2023.12.22 |
| 43. 렌즈계의 Stop과 Pupil들 (1) | 2023.12.01 |
| 42. 얇은 렌즈의 초점면과 초점 상 (1) | 2023.12.01 |



