


단색수차들(Monochromatic Aberrations)
근축광학에서는 물체평면에 있는 각점으로부터의 연필광들이 근축 상평면 에 있는 공액점으로 수렴되었다.
각각의 연필광선중 주광선은 이상적인 상점 의 위치를 결정하는 근축상면에서 교차되었다.
그러나 실제 광학계에서는 물 체로부터의 광선들이 모두 다 이상적인 상점에 수렴되지는 않으며, 주광선은 이상적인 상점과 교차하지 않을 뿐 아니라 상은 상평면에 형성되지 않는다.
완전 근축으로부터의 이러한 어긋남이 횡 수차들이다. 수차를 갖는 상은 형 태와 선명도에 결손을 나타낸다.
수차는 입사동 직경과 시야각(field angle)이 증가함에 따라 극적으로 증가된다. 단순광학계의 수차를 제한하려면 동(pupil) 의 직경이 작아야하는데 이는 또한 낮은 수치개구 값, 또는 큰 f/No 를 의미 하므로 이 또한 시스템의 제한 요소가 된다. 이런 시스템들은 회절번점들 이 크고 상은 흐려진다. 시야전체를 가로질러 밝고 날카로운 평면상을 얻으 려면 수차를 교정해야한다.
비록 삼각 함수적 광선 추적에 의하여 수차를 정밀하게 계산할 수 있지만 컴퓨터를 사용하지 않고 계산하는 것은 매우 지루한 일이다. Seidel은 상에 나타나는 결손을 구조적으로 해석하였다. 그는 구면수차, 코마수차, 비점수차, 왜곡수차, 파면만곡수차의 5가지 단색수차를 정의했으며, 굴절률과 개구직경, field angle등이 수차에 어떻게 영향을 끼치는지를 보여주었다.
3차이론(Third order theory)
각의 sine값은 다음과 같은 무한급수로 표현될 수 있다. 여기 α는 radians 값으로 쓰였다.
sin( α ) = alpha - ( α ^3)/3! + ( α ^5)/5! - ( α ^7)/7! + ...
근축방정식에서는 Snell의 법칙에서 각의 sine값들을 radian값으로 쓴 각 자 체의 값을 사용했다. 즉, 급수는 첫 항에서 중단되었고 nsina: = n' sin α 를 n' sin α ' 로 썼다. 근축광학은 급수전개식의 첫 항만을 사용하였기 때문에 1차 이론이라 부른다. 3차 이론에서는 처음 두 항들을 사용한다. 이것은 개구 가 크고 시계 각들이 더 큰 경우에 Snell의 법칙에 대하여 1차 이론보다 더 욱 좋은 근사를 나타낸다. 차수가 더욱 커지면 Snell의 법칙에 대한 근사는 더 좋아지고 빠르고 넓은 각을 갖는 광학계들에 대하여 더욱 정확한 계산이 된댜 매우 복잡한 광학의 수차방정식을 5차와 7차 근사에 기초한 식들이 사용된다.
얇은 렌즈의 구면수차
종 구면수차 LSA는 근축 상거리 u'와 동내의 어떤 높이 h로 입사된 광선 이 굴절된 후 광축과 교차된 거리(L')와의 차이이다. 즉, LSA = L' - u' 이다. L' 가 u' 보다 작을 때 구면수차는 미 교정 상태이다. LSA = TSA/tanθ' 이다.
LSA는
1)동내에서 광선의 높이의 제곱과,
2)렌즈의 bending이나 경사 인자 그리고,
3)물체의 위치 L 등에 의존하여 증가한다. 이 값들은 얇은 렌즈에서는 다음으로 주어진다.
L' = u' / Gu' + 1
여기서 G = 1 / L' = 1 / u' = h^2 / f^3 (AS^2 + BSP + CP^2 + D)
정리하면 LSA = L' - u' = - Gu'^2 / Gu' + 1
h^2 항은 광선 높이의 제곱에 대한 LSA의 의존성을 보여준다.
LSA의 렌즈 Bending에 대한 의존성은 다음으로 정의하는 형태인자 S를 사용하여 나타낸다. 여기서
S = r2 + r1 / r2 - r1
물체의 위치는 다음으로 정의하는 위치인자 P로 나타낸다. 여기서
P = u' + u / u' - u
다른 상수들은 렌즈의 굴절률 n의 함수이다.
A = n + 2 /8n(n - 1)^2
B = n + 1 / 2n (n -1)^2
C = 3n +2 / 8n
D = n^2 / 8 (n - 1)^2
구면수차와 렌즈 Bending
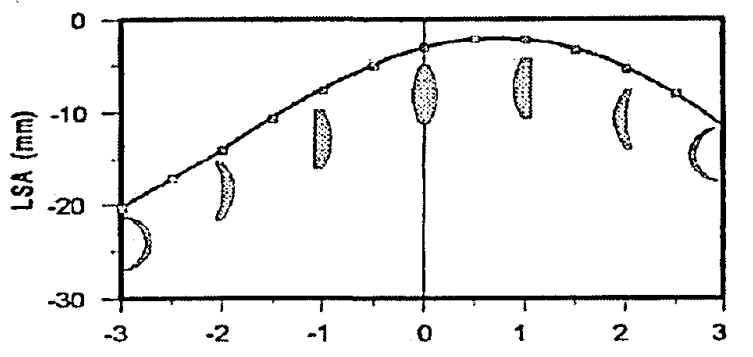
Bending의 함수로서 초점거리 50mm인 얇은 렌즈의 종 구면 수차(LSA)를 보여주는 그림이다.
LSA는 형태인자가 +0.5와 +1 사이의 값을 갖을 때 최소가 된다. 이와 같이 수 차가 작은 형태의 렌즈를 구하기 위하여
G = 1 / L' = 1 / u' = h^2 / f^3 (AS^2 + BSP + CP^2 + D) 식을 S에 대하여 미분한다.
h^2 / f^3, CP^2, D는 상수이므로, 수차가 작아지는 렌즈형태의 형태인자는
S = - BP / 2A 이다.
'Optics > Ray optics' 카테고리의 다른 글
| 49. Sine 조건 (1) | 2023.12.22 |
|---|---|
| 48. Coma 수차표기에 대하여 (1) | 2023.12.22 |
| 46. 광학 수차의 비교 (0) | 2023.12.22 |
| 45. 색 수차와 단색 광학 수차 (1) | 2023.12.22 |
| 44. 광선 수차란 무엇인가? (1) | 2023.12.22 |



