


코마는 하나의 물체점이 비축으로 이동하면서 크게 만들어지는 비대칭적 blur 이다. 이것은 렌즈 Zone과 함께 측 배율에 변화를 나타낸다. 구면수차 처럼 코마는 입사광선의 동(pupil)내의 높이의 h의 제곱에 따라 중가된다. 덧붙여서, 이후 설명하겠지만 코마는 계(field)각이나 물체의 높이와 함께 직접적으로 증가하기도 한다. 렌즈는 중심으로부터 가장자리로 나가면서 굴절력이 증가하는 것으로 생각할 수 있다. 순수 코마에서는 비 축점으로 부터 의 주광선은 상면의 높이 y'ideal 에 교차된다.


자오 단면의 꼭대기부분과 바닥부분을 지나는 광선들은 (土A)렌즈의 가장자 리 Zone에 의하여 굴절된댜 이 Zone은 가장 짧은 초점거리를 가지므로 따라 서 광선들은 y'ideal 보다 낮은 높이에서 만나게 된다. 꼭대기와 바닥보다 작은 개구 Zone에 연속적으로 입사된 광선들은 y'ideal 로부터 짧은 거리에서 상면의 자오 단면에 도달한다. 개구의 양쪽 즉 Sagittal 단면에 있는 가장 자리 광선 들 士 C은 그림에서처럼 자오 단면에서 교차된다. 士 B광선들은 사각광선들 이다. 士B와 士 D같은 모든 사각광선들의 반대쪽 상들은 상면의 한 점에서 만나게 되고 고리꼴 모양의 상을 형성한다
이제 아래 그림을 보자, 전체 고리들은 y'ideal 로부터 아래쪽으로 변위되어 있다. 이 과정은 연속적인 보다 작은 Zone들에 들어간 광선들에서도 반복된다. 이들은 점진적으로 작아져 y'ideal 에 접근하는 고리들의 계열을 이룬다. 그들의 포락선은 혜성처럼 보이게 된다. Tangential Coma 또는 ComaT 는 y'ideal 로부터 가장 큰 고리의 바닥 모서리까지의 거리이다. Sagittal Coma 또는 ComaS는 가장자리 고리상의 반경과 같다. Coma는 비대칭적 blur를 만들기 때문에 이 것은 매우 큰 불편을 끼치는 수차이다. 여기서 수차 다항식의 3차 comatic 항들을 구할 수 있다.
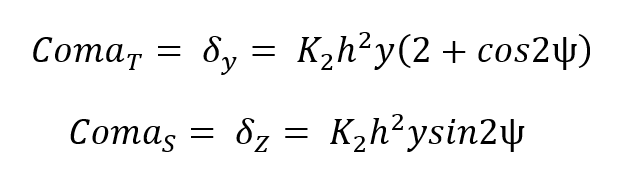
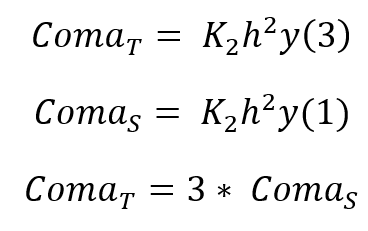
이제 가벼운 몸 풀기로 가볼까?
얇은 렌즈의 comatic blur 나 ComaT 의 길이는
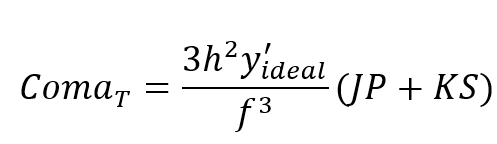
로 주어진다. 여기서, y' 는 이상적인 상 높이 이고
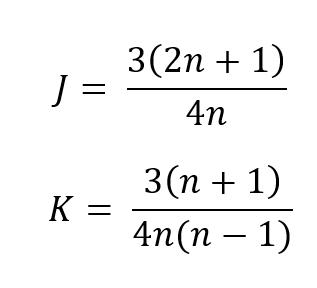
구면수차처럼 렌즈의 코마는 형태인자 S와 위치인자 P에 의존한다. 그러나 얇은 렌즈의 코마는 렌즈를 bending하여 영으로 만들 수 있다. 코마 에 대한 렌즈의 가장 좋은 형태는 아래의 식
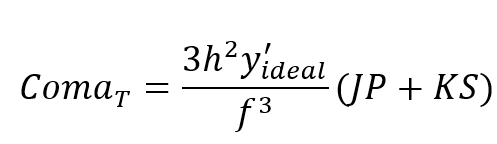
(Jp+Ks)항을 0으로 둠으로써 구해진다. 형태인자에 대하여 풀면 다음과 같다.
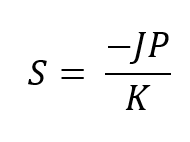
'Optics > Ray optics' 카테고리의 다른 글
| 50. 비점수차 (Astigmatism)와 Petzal 곡률 (1) | 2023.12.22 |
|---|---|
| 49. Sine 조건 (1) | 2023.12.22 |
| 47. 단색수차, 그리고 3차 이론과 구면수차 (1) | 2023.12.22 |
| 46. 광학 수차의 비교 (0) | 2023.12.22 |
| 45. 색 수차와 단색 광학 수차 (1) | 2023.12.22 |



