


비점수차 (Astigmatism)
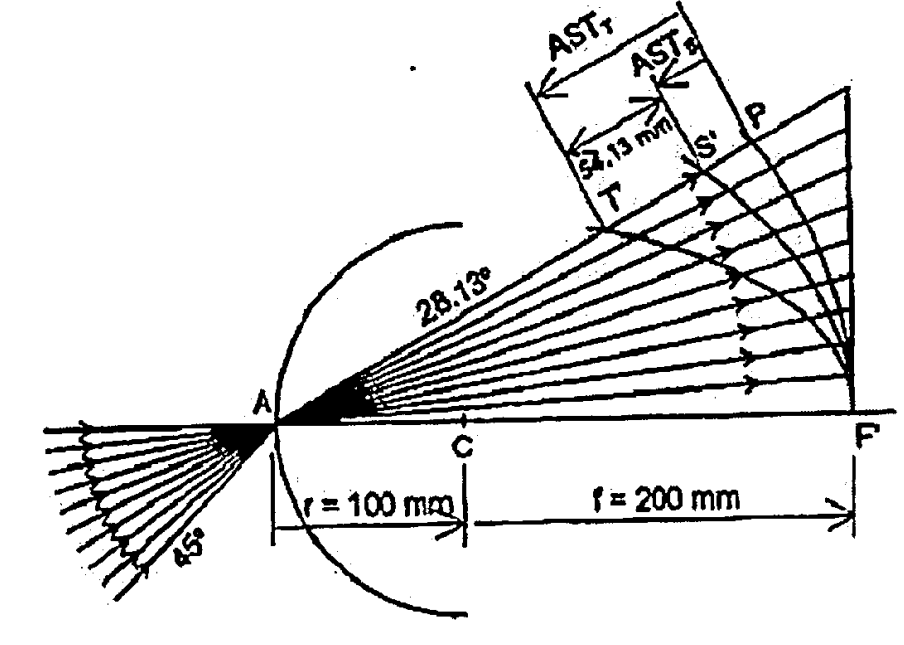
구면렌즈는 비축 점 물체의 상을 비점형태로 만든다. 어떠한 점 Q로부터 렌즈에 자오(tangential)광선과 구결(sagittal)광선을 보낸다고 하자. 자오(Tangential)과 구결(sagittal) 연필광들은 렌즈로부터 다른 거리에서 주광선과 교차되어 각각 초점선분 T' 와 S'를 형성한다. 교정이 안된 상태에 서 초점선분들은 근축상면의 앞에 떨어진다. 상면과 S' 사이거리, 그리고 T' 과 S'사이간격은 물체의 높이와 함께 증가된다. Field 내에 있는 어떤 점에서 비점수차는 주광선을 따라 측정된 T' 와 S' 사이의 간격으로 주어진다. 주광 선을 따라 자오(tangential)과 구결(sagittal) 비점 상 거리를 그리면 아래 그림과 같다.
구 굴절면에 대한 sagittal 상 거리S'와 tangential 상 거리 T'계산을 하 기위한 Coddington 방정식은 다음과 같다.
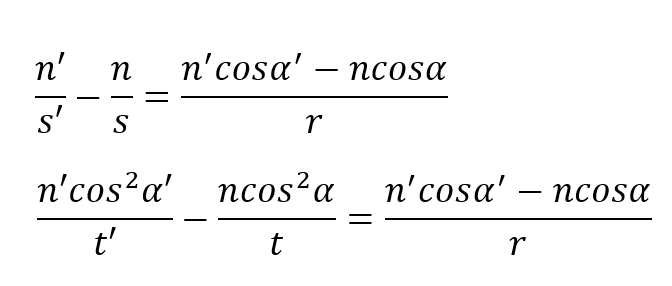
물체거리 S와 t그리고 공액 상 거리 s' 와 t’ 들은 주광선을 따라 측정된다.
Petzal 곡률
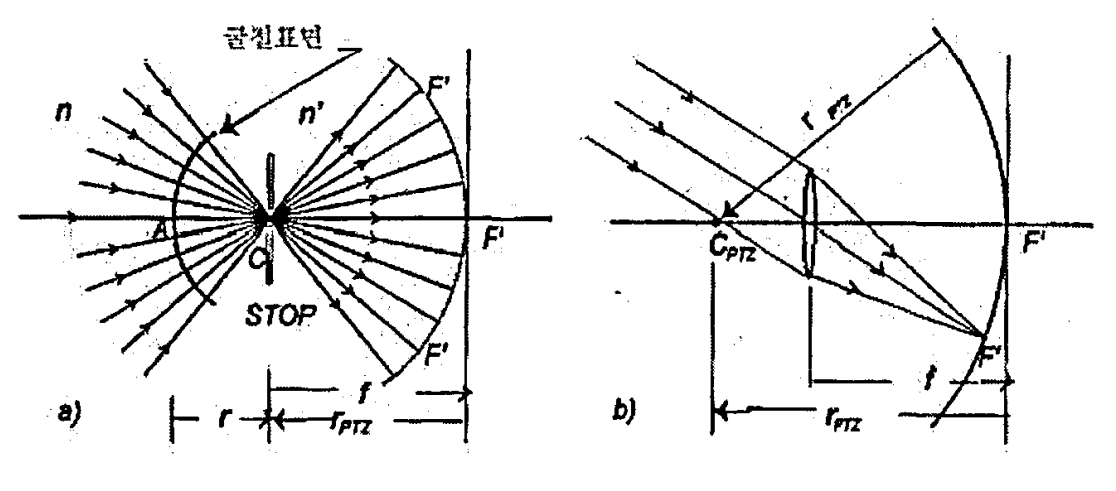
이상적으로는 카메라나 프로젝터들이 만든 상은 평면을 형성해야 한다. 그러나 보통의 광학계들은 평면상들을 형성하지 못한다. 가장 간단한 예로써 구 굴절면에 의해 형성된 상을 생각해보자. 작은 개구스톱을 구굴절면의 곡 률중심에 둘 때 단일광축은 촌재하지 않는다. 모든 주광선들이 하나의 광축 과 부합되는 것으로 고려될 수 있다. 넓은 field의 원거리 물체는 C에 중심 을 두고 F'에 정점이 있는 구면위에 상이 있게 된다. 이 때 상면은 Petzval 면이라 부른댜 Petzval 면의 곡률 반경은 rPtz = F'C = -f 이다.
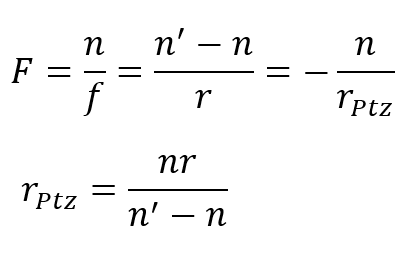
Petzval 곡률은

얇은 렌즈는 두개의 표면들을 가지므로 K=2이다. 따라서 첫 번째 면에 서 j = 1 , ni = 1 , nj = n (렌즈 굴절률) 이다. 두 번째에서 j = K , 따 라서 nK = n , n'K = 1 이다. 이 값들을 K개의 연속 표면들에 대한 상의 Petzval 곡률식에 대입하면

이 된다. 얇은 렌즈의 Petzval 면의 반경은

이때 평면 상면에 대한 Petzval 조건을 고려한다면
오목렌즈가 만드는 발산 파면의 곡률은 볼록렌즈가 만드는 수렴 파면의 곡률과 반대이다. 렌즈를 조합 하여 상을 평면으로 만들려면 다음의 Petzval 조건이 만족 될 수 있어야 한다.
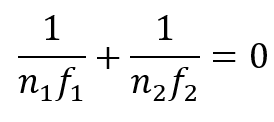
이 조건은 렌즈들 간의 분리된 간격에 의촌 하지 않는다는 점이 홍미롭다. 다른 말로 하면 볼록 렌즈의 곡률 반경은 오목렌즈를 상평면이나 상평면 근 처에 둠으로서 교정 될수 있다는 의미가 된다. 그러한 렌즈 들은 field flatteners 라 부른다. 만일 비점 수차가 교정되었다면 그 상면은 Petzval 면이다.
'Optics > Ray optics' 카테고리의 다른 글
| 49. Sine 조건 (1) | 2023.12.22 |
|---|---|
| 48. Coma 수차표기에 대하여 (1) | 2023.12.22 |
| 47. 단색수차, 그리고 3차 이론과 구면수차 (1) | 2023.12.22 |
| 46. 광학 수차의 비교 (0) | 2023.12.22 |
| 45. 색 수차와 단색 광학 수차 (1) | 2023.12.22 |



