


균일한 매질 내에 있는 렌즈에 대한 얇은 렌즈 공식은 렌즈의 두 굴절 표면 각각에 구 굴절면에 대한 굴절 방정식을 적용하여 구하면 된다.
제 1면에서는 굴절에 의하여, 제2면에 대하여 물체역할을 하는 상을 만든다. 즉 제1면의 상은 제2면에 대하여 물체역할을 한다. 아래의 그림에서는 렌즈 두께를 과정하여 표현하였지만 렌즈 두께 d를 0으로 두고 계산해보자.
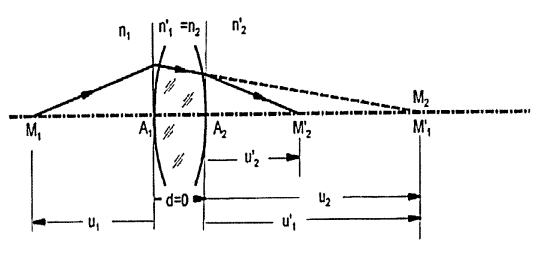
얇은 렌즈 가정에 따라 d=0으로 취급하므로, A1점과 A2점을 일치시켜 A점으로 둔다. M1 점은 렌즈에 의하여 결상되는 물체이다. 물체거리 u1 = AM1이다.
렌즈의 제1면에서 굴절된 후에 상 M1’는 u1' = AM1’ 거리에 형성된다. 비록 상이 렌즈의 오른쪽에 나타나게 되지만, 이것은 렌즈매질에 관계되어 광선은 굴절되게 된다. 상점 M1’는 렌즈의 두 번째 면에 대하여 허물체로서 작용한다.
따라서 이것을 M2로 바꿔서 쓴다. 두 번째 표면에서 굴절된 후에 최종상 M2'를 형성한다. 위 그림은 M1과 M1' 또한 M2와 M2'와 같이 공액점임을 보여준다. 결론적으로 M1과 M2는 서로 공액점이다.
렌즈의 첫 번째 면에 대한 굴절방정식은
\[ \frac{n_1'}{u_1'} = \frac{n_1}{u_1} + \frac{(n_1' - n_1)}{r_1} \]
그런데 앞에서는 \( n_1' = n' \) 그리고 \( n_1 = n \)으로 표기했다. 또한 상거리 \( u_1' \)는 물체거리 \( u_2 \)와 같다. 따라서 위 식을 다음처럼도 쓸 수 있다.
\[ \frac{n'}{u_2} = \frac{n}{u_1} + \frac{(n' - n)}{r_1} \]
제 2면에서의 굴절 방정식은
\[ \frac{n_2'}{u_2'} = \frac{n_2}{u_2} + \frac{(n_2' - n_2)}{r_2} \]
이 방정식은 다음으로 쓸 수 있다.
\[ \frac{n}{u_2'} = \frac{n'}{u_2} - \frac{(n' - n)}{r_2} \]
이제 두 식을 \( u_1 = u \), \( u_2' = u' \)로 바꿔서 다시 한번 써보자.
\[ \frac{1}{u'} - \frac{1}{u} = \frac{(n' - n)}{n} \left( \frac{1}{r_1} - \frac{1}{r_2} \right) \]
구굴절면에서 정의된 것처럼 무한에 있는 물체의 상은 렌즈의 제2초점 \( F' \)에 형성된다. 제1초점 \( F \)에 있는 물체는 무한에 상을 형성한다. 즉, 물체 거리 \( AM = -FA \) 또는 \( u = -f \) 일 때 상거리 \( u' \)는 무한이다. \( u \)와 \( u' \), 이 값들을 위 식에 대입하면 다음과 같은 렌즈제작자 공식을 구할 수 있다.
\[ \frac{1}{f} = \frac{(n' - n)}{n} \left( \frac{1}{r_1} - \frac{1}{r_2} \right) \]
렌즈 제작자 공식에서 \( n' \)는 렌즈의 굴절률이고, \( n \)은 렌즈가 놓여있는 주변 매질의 굴절률이다.
이를 통해서 우리가 이미 알고 있는 얇은 렌즈 공식은
\[ \frac{1}{u'} = \frac{1}{u} + \frac{1}{f} \]
'Optics > Ray optics' 카테고리의 다른 글
| 39. 비축상점의 작도법과 측(횡) 배율 (1) | 2023.11.30 |
|---|---|
| 38. 초점 거리 (0) | 2023.11.29 |
| 36. 렌즈의 광학적 중심 (1) | 2023.11.28 |
| 35. 볼록렌즈와 오목렌즈 (0) | 2023.11.28 |
| 34. Smith-Helmholtz 공식, Lagrange 불변량 (1) | 2023.11.27 |



