

38. 초점 거리Optics/Ray optics2023. 11. 29. 21:54
Table of Contents
반응형

제 2초점 \( F' \)는 광축과 렌즈의 두 번째 초점면과의 교차점에 놓여있다.
\( u \)가 무한일 때 상점 \( M' \)는 \( F' \)과 부합되므로 \( AM' = AF' \)이다.
이전 포스팅의 얇은 렌즈 방정식에 의해 \( u' = f \) 또는 \( AM' = FA \) 이다.
결과적으로 \( FA = AF' \), 그러나 \( AF' = -F'A = -f' \) 이므로 따라서
\[ f = -f' \]
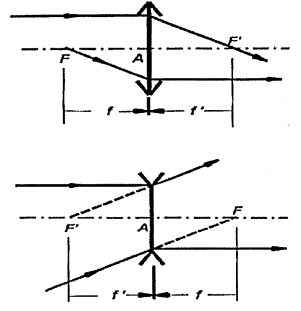
이식의 의미는 얇은 렌즈의 초점들은 렌즈의 반대쪽들에 있지만 같은 렌즈로 부터의 거리는 같음을 의미한다.
볼록렌즈의 경우 제1초점F는 렌즈 의 앞쪽에 있고 제1초점거리 f는 양의 값을 갖는다.
제2초점F는 렌즈의 뒤 쪽에 있고 f 는 음의 값이댜 오목렌즈의 경우에는 초점들의 순서는 역으로 된다.
제1초점거리 f는 음의 값을 갖고 f는 양의 값을 갖는다.
반응형
'Optics > Ray optics' 카테고리의 다른 글
| 40. 얇은 렌즈에 의한 상의 형성 (0) | 2023.11.30 |
|---|---|
| 39. 비축상점의 작도법과 측(횡) 배율 (1) | 2023.11.30 |
| 37. 렌즈 공식 중간 정리 (0) | 2023.11.29 |
| 36. 렌즈의 광학적 중심 (1) | 2023.11.28 |
| 35. 볼록렌즈와 오목렌즈 (0) | 2023.11.28 |



