

34. Smith-Helmholtz 공식, Lagrange 불변량Optics/Ray optics2023. 11. 27. 14:51
Table of Contents
반응형

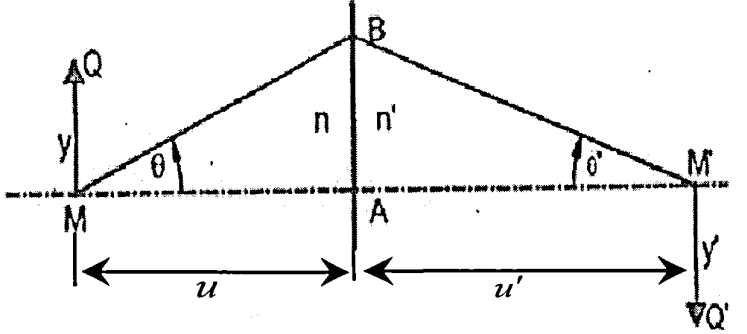
위 그림에서보면 물체광선 MB는 굴절된 광선 BM'가 되고 광축과 함께 삼각형 MBM'를 형성한다.
Sine 법칙에 따르면
\[ \frac{\sin \theta}{\sin \theta '} = \frac{BM'}{BM} \]
이 되는데 이 식을 근축광선에 대한 가정을 사용하여 등가식으로 다시 쓰면
\[ \frac{\theta}{\theta '} = \frac{u'}{u} \]
측 배율에 대한 방정식을 다시 쓰면
\[ \frac{u'}{u} = \frac{n' y'}{n y} \]
위 식들을 결합하여 Smith-Helmholtz 공식, Lagrange 불변량을 구할 수 있다.
\[ n' y' \theta ' = n y \theta \]
이 식에 따르면 광학계 내에 광학적 표면들이 얼마나 많이 있던지 간에 굴절률과 물체 높이와 광축 주변에 있는 광선(axial ray)들의 기울기의 곱은 일정한 값이 된다.
반응형
'Optics > Ray optics' 카테고리의 다른 글
| 36. 렌즈의 광학적 중심 (1) | 2023.11.28 |
|---|---|
| 35. 볼록렌즈와 오목렌즈 (0) | 2023.11.28 |
| 33. 구 굴절면의 초점면과 상 (2) | 2023.11.27 |
| 32. Newtonian 방정식 (1) (2) | 2023.11.26 |
| 31. 평면 굴절면에서 상 방정식 (1) | 2023.11.25 |



