


초점은 초점면이라 부르는 광축에 수직인 횡 평면에 놓여있다.
F를 지나는 첫 번째 또는 일차초점면은 무한에서 공액상면을 갖는다.
무한 물체평면은 F’에 있는 제2초점면에 대하여 공액이다.
무한거리의 비축물체 S는 굴절면에 시준된 광선들을 보낸다.
아래 그림에서 보는바와 같이 제 2초점면에서 상 S’의 높이(크기)를 구하게 된다.
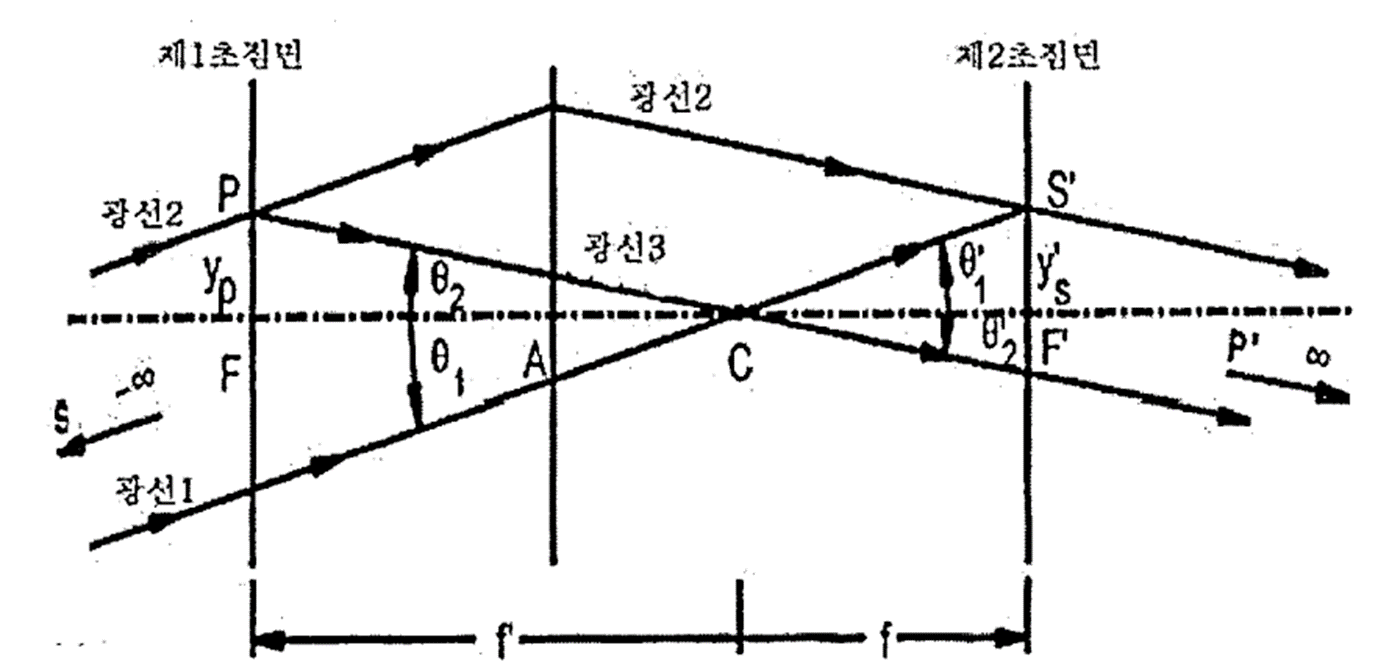
중심 C를 지나는 광선1은 편향되지 않는다.
이 광선은 평행하게 진행한 광선2와 제2초점면의 S’에서 교차된다.
상의 크기는 \( y'_s = F'S’ \)이다, 광선 1은 \( \theta_1 \)의 기울기를 가지므로 삼각형 \( CF'S' \)에 의하여
\[ \tan \theta_1 = \frac{F'S’}{CF'} = \frac{y'_s}{f} \]
또는
\[ y'_s = f \tan \theta_1 \]
각이 작은 경우에는
\[ y'_s = f \theta_1 \]
이 식은 구 굴절면에 의하여 형성된 무한거리에 있는 크기가 있는 물체의 상의 크기를 말해준다.
상의 크기는 광선 기울기와 초점거리의 곱셈과 같다.
제1초점면에 있는 P점은 비축물체를 나타낸다.
P점에서 나와 C를 지나는 광선 3은 편향되지 않게 되고 상공간 내에서 광선 2에 평행하게 진행하게 된다.
이 광선들은 무한에서 상 P’를 만들게 된다.
\[ \tan \theta_2 = \frac{FP}{CF} = \frac{y'_p}{f} \]
또는
\[ y'_p = f \tan \theta_2 \]
각이 작은 경우에는
\[ y'_p = f \theta_2 \]
'Optics > Ray optics' 카테고리의 다른 글
| 35. 볼록렌즈와 오목렌즈 (0) | 2023.11.28 |
|---|---|
| 34. Smith-Helmholtz 공식, Lagrange 불변량 (1) | 2023.11.27 |
| 32. Newtonian 방정식 (1) (2) | 2023.11.26 |
| 31. 평면 굴절면에서 상 방정식 (1) | 2023.11.25 |
| 30. 측 배율 또는 횡 배율 (1) | 2023.11.25 |



