


프리즘은 평면을 갖고 있는 투명물질이거나 유리의 block 형태이다.
가장 일반적인 프리즘은 3각 단면을 갖는 기둥구조이다.
만일 프리즘의 평편한 한 쪽 면 방향으로 빛이 입사된다면, 입사각 \( \theta \) 에 의존하여 변화된 편향 각 \( \delta \) (프리즘에 입사하여 굴절되어 나가는 광선이 나타내는 편향각들의 총계 값) 값을 구하게 된다.
입사각을 변화시켜 측정한 편향각 값들 중에서 최소 크기의 편향각 값을 최소 편향 각 \( \delta_{\text{min}} \)이라 하며, 이는 프리즘 유리 재질의 굴절률 \( n \)과 프리즘 정각(꼭지각) \( A \)에 의존한다.
\( \delta_{\text{min}} \)과 \( A \)를 측정하면, 이 변수들의 함수로써 굴절률 \( n \)을 구할 수 있다.
또한 \( n(\delta_{\text{min}}, A) \)는 프리즘형태의 미지의 광학 시료 물질이나 유리 재질 프리즘의 굴절률을 실험적으로 결정하는데 사용될 수 있다.
굴절률 함수인 최소 편향각 \( \delta_{\text{min}} \)과 꼭지각 \( A \)에 대한 의존성 관계를 정확하게 구해보자.
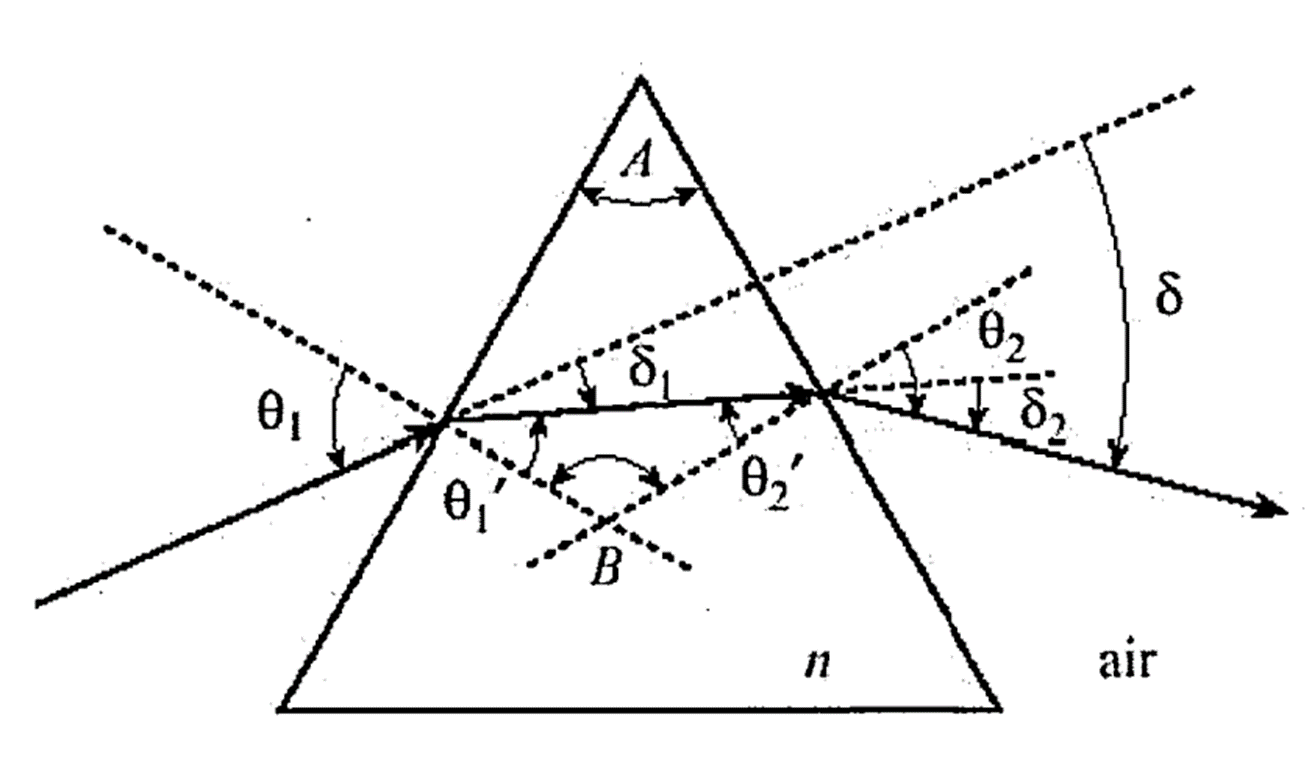
입사광선의 편향각의 총합은 제1면에서의 편향각과 공기 중으로 나가는 제 2면에서의 편향각의 합이다.
따라서 \( \delta = \delta_1 + \delta_2 \)이다. 또한 그림에서 보는 바와 같이 프리즘의 입사 측 제1면 경계면과 투과해 나가는 제2면 경계면을 통과하는 광선들이 수직선에 대하여 만드는 입사각과 그의 반대 각들이 서로 같아야 하므로 \( \theta_1 = \theta_1' + \delta_1 \)과 \( \theta_2 - \delta_2 = \theta_2' \)가 되고
제 1면과 2면에서의 편향각의 함수로 정리하면 \( \delta_1 = \theta_1 - \theta_1' \)와 \( \delta_2 = \theta_2 - \theta_2' \)이 된다. 총 편향각 \( \delta = ( \theta_1 + \theta_2) - ( \theta_1' + \theta_2') \)이 된다.
여기서는 상세히 증명하지 않았지만 \( \theta_1 = \theta_2 \)일 때 \( \delta = \delta_{\text{min}} \)이 됨을 알 수 있다.
이 결과로부터 \( \delta \)를 \( \theta_1 \)의 함수로 쓸 수 있게 되며 도함수를 취하고 이것을 zero로 두어 최소값을 구한다.
따라서 \( \delta_{\text{min}} = 2( \theta_1= \theta_1') \)가 되고, 프리즘 정각과 양면에 대한 법선이 만드는 4-변형 다각형의 내각의 합은 360도이다.
즉 \( A + B + 90 + 90 = 360 \)이므로, \( A + B = 180 \)이고 삼각형의 내각의 합은 180이므로 \( B + \theta_1' - \theta_2' = 180 \)이다. 따라서 \( A = \theta_1' - \theta_2' \)이 된다.
따라서 \( \delta = \delta_{\text{min}} \)일 때, \( A = 2 \theta_1' \)이 된다.
최종적으로는 Snell의 법칙은 \( \sin \theta_1 = n \times \sin \theta_1' \)로 쓸 수 있게 되므로 \( \delta_{\text{min}} \)과 \( A \)의 항으로 굴절률을 쓰면 프리즘의 굴절률은 \( n(\delta_{\text{min}}, A) = \frac{\sin{(\delta_{\text{min}}+A)/2}}{\sin{A/2}} \)로 표현된다.
정각 \( A \)가 매우 작은 프리즘에서는 편향각 \( \delta \)도 또한 작으므로, sine 함수에 대하여 Small-angle 근사를 사용하여 식을 더 간편하게 쓸 수 있다.
\( \Phi \)가 작을 때 \( \sin(\Phi) = \Phi \)이 근사를 사용하는 경우에는 최소 편향각은 \( A \)와 \( n \)만을 알면 계산될 수 있다.
프리즘의 근사적인 최소 편향각은 \( \delta_{\text{min}} = A(n-1) \)이 된다.
최소 편향각은 일정하게 한 방향으로 프리즘을 조명하는 입사광선(예: 레이저)에 대하여 프리즘을 조심스럽게 회전시킴으로써 측정될 수 있으며, 이때 프리즘을 굴절하여 통과하는 광속의 편향각은 제1면에 대한 입사각이 증가함에 따라 감소되는데 입사각이 어떤 값 이상이 되면 편향각이 또 다시 증가되는 입사각이 있게 된다.
이때의 편향각이 최소 편향각이 된다.
'Optics > Ray optics' 카테고리의 다른 글
| 21. 평면 경계면에서의 반사 - 거울 (1) | 2023.11.18 |
|---|---|
| 20. 프리즘에서의 분산 (0) | 2023.11.18 |
| 18. 평행 평면판을 통과하는 광선의 추적 (0) | 2023.11.16 |
| 17. 평면 표면에서의 근축 굴절 (2) (0) | 2023.11.15 |
| 16. 평면 표면에서의 근축 굴절 (1) (0) | 2023.11.14 |



