


평행 매질에서의 광선 경로
창문의 유리판이나 물이 담긴 잔은 평행한 경계들을 갖고 있다.
이런 매질들에서 광선의 경로는 Snell의 법칙을 반복적으로 적용하여 구할 수 있다.
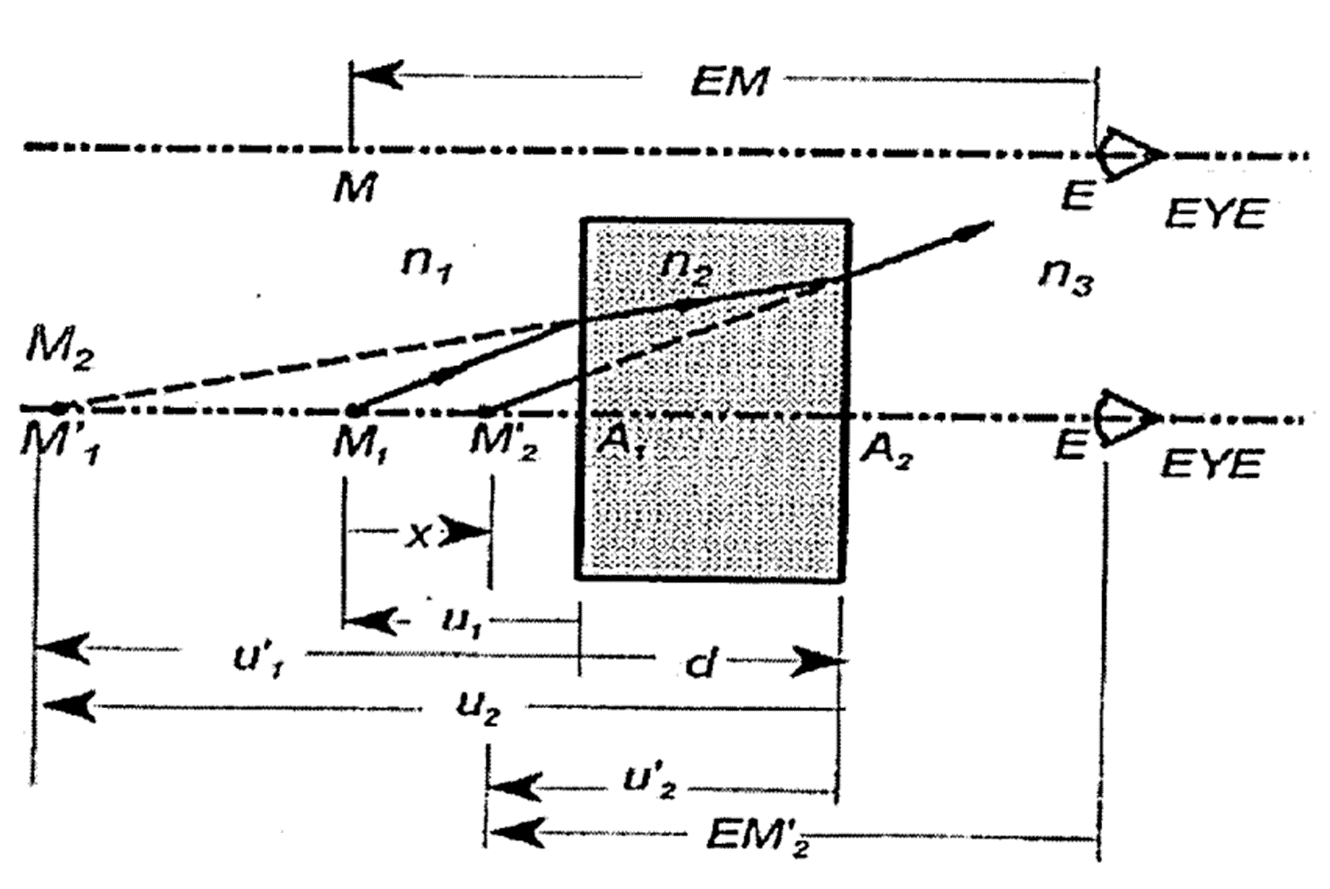
평행 광선이 입사된다고 하고, 아래의 그림을 참고해서 첫 번째 경계에서 입사광선의 입사각과 평면 매질의 굴절률을 각각 \( \alpha_1 \)과 \( n_1 \)이라 하자.
두 번째 경계에서는 숫자를 바꿔 표기한다.
그러면 Snell의 법칙에 의하여
\[ n_j \sin \alpha_j = n_j' \sin \alpha_j' \]
여기서 j는 광선이 통과 하는 경계면들을 나타낸다.
첫 번째 면에서 j =1, \( n_1 \sin \alpha_1 = n_1' \sin \alpha_1' \) 두 번째 면에서 j =2, \( n_2 \sin \alpha_2 = n_2' \sin \alpha_2' \)
그런데 \( n_1' \sin \alpha_1' = n_2 \sin \alpha_2 \) 이므로 \( n_1 \sin \alpha_1 = n_2' \sin \alpha_2' \) 가 된다. 따라서 \( \alpha_1 = \alpha_2' \)
즉 두 번째 경계에서 매질을 통과해 나가는 각은 첫 번째 면에서의 입사각과 같다.
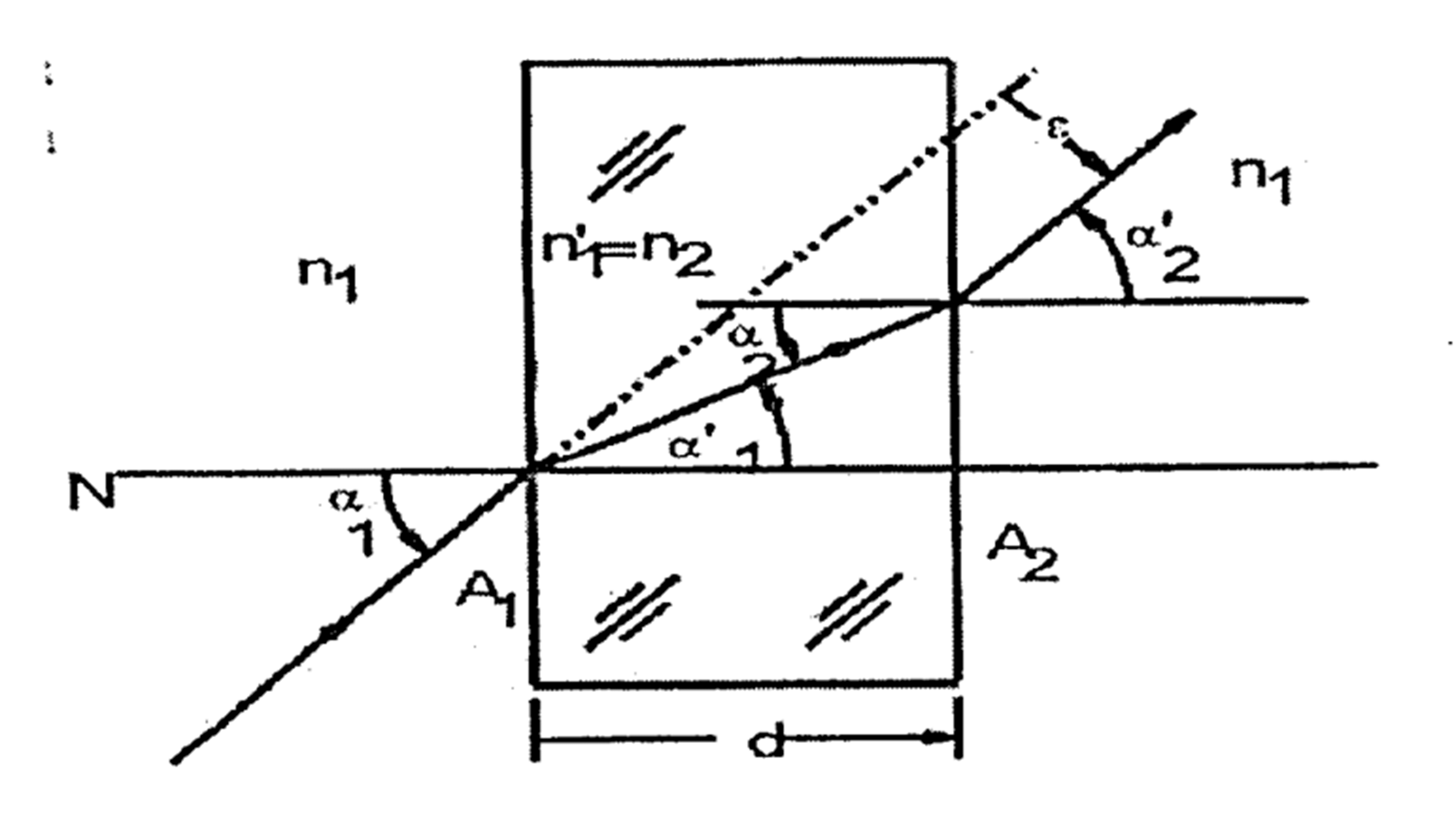
그러면 위 그림을 참고하면 두께 d인 평판 매질을 입사각 \( \alpha \)로 입사하여 투과해 나가는 광선의 경로를 구해보자.
평판을 투과해 나가는 광선은 거리 e 만큼 변위된다.
광선의 경로 S는 두 직각 삼각형의 긴 변이 된다.
그림에서 윗 부분 삼각형을 보면 \[ e = S \sin( \alpha - \alpha' ) \]
아래 삼각형에서는 \( S = \frac{d}{\cos \alpha'} \)
변위 e는 따라서 \( d \sin ( \alpha- \alpha')/\cos \alpha' \)이다.
'Optics > Ray optics' 카테고리의 다른 글
| 20. 프리즘에서의 분산 (0) | 2023.11.18 |
|---|---|
| 19. 프리즘을 통과하는 광선의 굴절 (0) | 2023.11.17 |
| 17. 평면 표면에서의 근축 굴절 (2) (0) | 2023.11.15 |
| 16. 평면 표면에서의 근축 굴절 (1) (0) | 2023.11.14 |
| 15. 평면 굴절면을 통한 광선의 굴절 (1) | 2023.11.13 |



