


\(\lambda\nu\)
빛의 파동이론에 의하면 스펙트럼의 색들은 각각 파장 \(\lambda\)와 진동수 \(\nu\)가 다른 값을 갖는다. 빨간색 스펙트럼은 파장이 길어 약 700nm 정도의 파장을 갖으며, 보라색 스펙트럼은 파장이 짧아 약 400nm 정도의 파장을 갖는다. 진공 중에서는 모든 파장의 빛들이 동일한 일정속도 \(C\)로 이동하며 광속 \(C\)는 파장과 진동수의 곱으로 주어진다.
\( C = \nu \cdot \lambda = 300,000 \, \text{km/sec} \)
유리나 공기와 같은 매질의 굴절률은 매질 속에서의 광속 \(V\)와 진공 중에서의 광속 \(C\)의 비율과 같다. 그런데 매질 속에서의 광속은 진공 중에서의 광속보다 작다 (\(V < C\)). 따라서 매질의 굴절률은 단위값 1보다 큰 값이 된다.
\( n = \frac{C}{V} \)
Snell의 법칙은 광선의 입사각과 굴절각의 Sine값의 비가 상수 값이 됨을 의미하는데 이 상수는 매질의 굴절율의 비와 같다.
\( \frac{\sin(\theta)}{\sin(\theta')} = \frac{n'}{n} \)
보통의 광학 매질에서는 빛의 파장에 따라 사각으로 입사한 광선의 투과된 굴절각이 변화되는데 이는 파장에 따라 진행속도가 다르기 때문이다. 결론적으로, 매질의 굴절률은 빛의 파장에 따라 다르게 된다.

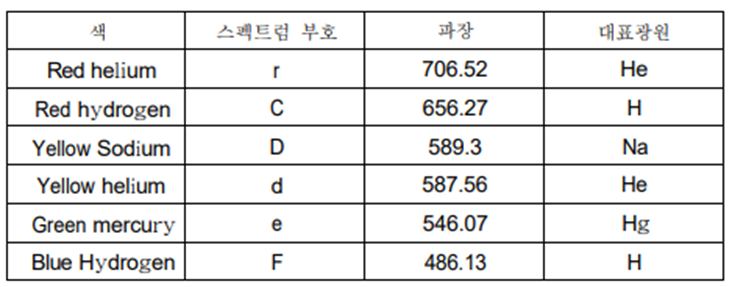
가장 작게 편향되는 파장이 킬은 빛에 대한 굴절률은 짧은 파장들의 굴절률보다 작다. Joseph van Fraunhofer는 태양광의 스펙트럼이 백열전구나 가열한 고체 물질의 스펙트럼처럼 완전히 연속되지 못하고 부분적으로 아주 좁은 어두운 선들이 그 스펙트럼에 존재함을 발견했다. 그는 이 어두운 스펙트럼선들은 태양의 광구 주변부 가스 층에서 빛을 흡수하여 발생한 것임을 밝혔다. 이 스펙트럼선들은 Fraunhofer선이라 부르며 분광학에서는 각각의 색 스펙트럼에 부호를 붙여 표기한다. 광학유리의 굴절률은 빛의 파장에 의존한다. 따라서 Fraunhofer선에 해당되는 파장의 빛들에 대한 굴절률은 \(nd, nF, ne\)등으로 표시한다.
한 예로 일반적으로 많이 사용하는 BK7 유리의 굴절률은 \(nd = 1.5168, nF = 1.52238, nc = 1.51432\)로 주어진다. 만일 굴절률 값이 \(nd\)로 주어졌고 특별한 다른 부호가 표시되어 있지 않다면 이는 일반적으로 helium 기체의 방전 발광 선 스펙트럼들 중에서 노란색의 빛(파장 d:587.56nm)에 대한 굴절률인 것으로 이해하면 된다. 광학유리로 사용되는 유리들은 굴절률이 큰 유리와 작은 유리 등 다양하여서 광학유리의 굴절률은 1.44로부터 2.04 사이의 값을 갖는다.
유리의 분산능 \(W\)는 \(W = \frac{nf - nc}{nd - 1}\)로 주어진다.
BK7 유리의 분산능은 0.015595이다. 더욱 일반적으로는 유리의 분산은 Abbe 수 \(V\)를 사용하여 나타낸다. Abbe 수는 분산능의 역수로써,
\(Vd = \frac{nd - 1}{nF - nC}\)
Vd는 d, F, C 파장들에 대한 Abbe 수이다. 가시광 영역에서 광학 유리들의 Abbe 수는 20으로부터 100 사이의 값을 갖는다.
BK7 유리의 Abbe 수는
\(Vd = \frac{1.5168 - 1}{1.522378 - 1.514324} = 64.17\)
nF-nC 값을 평균분산이라 부른다.
BK7유리에 대한 nF-nC 값은 0.00800이다.
광학유리들은 6자리 숫자로 광학상수들을 표기하는데 한 예로 BK7유리는 517642로 쓴다.
이 6자리 중 앞3자리 517은 BK7유리의 nd값 중 소수점 이하 3자리의 값이고,
뒤의 642는 소수점을 뺀 Abbe수의 첫 3자리 수 이다.
'Optics > Ray optics' 카테고리의 다른 글
| 22. 평면경계를 투과한 광선의 굴절현상: 근축광선들 (1) | 2023.11.19 |
|---|---|
| 21. 평면 경계면에서의 반사 - 거울 (1) | 2023.11.18 |
| 19. 프리즘을 통과하는 광선의 굴절 (0) | 2023.11.17 |
| 18. 평행 평면판을 통과하는 광선의 추적 (0) | 2023.11.16 |
| 17. 평면 표면에서의 근축 굴절 (2) (0) | 2023.11.15 |



