


물체가 평면 굴절면 근처에 놓여 있을 때 형성된 상에 대하여 생각해 보 자. 거울(반사)경계에서처럼 먼 단일 점광원 물체 O를 고려해 보자. 아래 그림에서 상의 위치에 대하여 일반적 규칙을 적용하면 : (1) 점 O로부터의 광선들을 추적하고, (2) Snell의 법칙을 적용하고, (3) 광선들이나 광선의 연장선들이 교차한 점들을 찾는다.

그림에서 보는바와 같이 여기서는 공통 교차점이 없음을 보게 되는데, 이는 실제 상이 그곳에 없음을 의미한다. 만일 2개의 광선만을 추적하게 되면 어리석게도 그곳에 상점이 있을 것으로 생각하게 된다. 그러나 2개 이상의 광선들이 교차하는 점도 없고 실제 상점은 그곳에 없다. 단지 "Image blur(불 분명한 상)”이 있거나, 또는 다중 교차점들이 발생된 영역이 있게 된다.
평면거울의 경우를 제외하고는 실제로 상을 구하기는 쉽지 않다. 그러나 특별한 상황에서는 매우 선명한 근사적인 상(단지 약간 선명치 않는)을 얻을 수 있다. 근축광선들(Paraxial rays)만 고려하면 상의 흐려짐(blur)이 작아진 근사적인 상을 구 할 수 있다.
근축광선: 상을 형성하는 광학계의 중심(광학)축 근처에 있는 광선들로써 광 축과의 사이 각이 작은 광선들이다.
굴절경계에서 광축은 시야 선을 따르며, 물체를 똑바로 내려 보는 방향이 평면 경계에 대하여 법선(수직)이 된다. 근축광선들의 경우에 Snell의 법칙 은 간단히 쓸 수 있다. 특히, \( \theta \ll \frac{\pi}{2} \) 일때, \( \sin \theta = \tan \theta = \theta \) ( \( \theta \)은 radian 값)
Snell의 법칙은 근사적으로 \( ni \theta_i = nt \theta_t \)로 쓸 수 있게 된다.

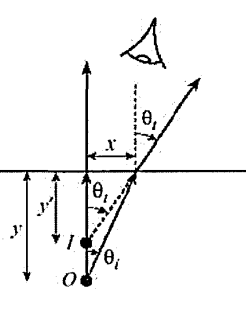
근축광선들에서는 "blur"나 여러 광선들의 교차점의 위치가 퍼지는 것이 매 우 작댜 따라서 단일상점 I의 위치를 근사적으로 구할 수 있다. 그림에서 처럼 경계에 대하여 수직인 광선을 포함한 2개의 광선들만을 추적하여 상 점을 구한다. 그림 에서 \( \tan \theta_i = \frac{x}{y} \) 이고, \( \tan \theta_t = \frac{x}{y'} \) 이므로, Snell 의 법칙의 근사적 형태 \( ni \frac{x}{y} = nt \frac{x}{y'} \) 로부터 \( y' = \frac{nt}{ni} \times y \) 이 되고, 따라 서 상점 y'의 깊이는 다음으로 주어진다.
y' = \( {nt}{ni} \times y \)
'Optics > Ray optics' 카테고리의 다른 글
| 24. 구형 경계면에서의 반사 (1) | 2023.11.22 |
|---|---|
| 23. 프리즘을 사용한 상의 방위 바꾸기 (1) | 2023.11.21 |
| 21. 평면 경계면에서의 반사 - 거울 (1) | 2023.11.18 |
| 20. 프리즘에서의 분산 (0) | 2023.11.18 |
| 19. 프리즘을 통과하는 광선의 굴절 (0) | 2023.11.17 |



