


곡면 경계에서는 원래 물체와 비교할 때 이그러(변형된)지고 확대된(또는 축소된)상이 형성될 수 있을 뿐만 아니라, 또한 공간 내에서의 위치와 방위가 다르게 될 수 있기 때문에 곡면 경계면에 의한 결상은 더욱 복잡해진다. 그 러나 이러한 차이는 또한 곡면 경계를 더욱 홍미롭게 한다! 사실, 렌즈와 같은 아주중요한 기초광학 소자들은 보통의 경우 구와 같은 곡률의 경계면을 이루고 있음을 보게 될 것이다.
먼저 볼록 구면형태의 반사 경계면에 의해 만들어 지는 단일 점 물체 0의 상점 I를 생각해 보자.
이 경우에는 일반적 규칙을 적용하여 상점을 구할 수 있다:
(1) 물체 점으로부터 2개의 광선들을 추적한다.
(i) 하나는 곡면경계면에 수직이고,
(ii) 다른 하나는 곡면경계면에 대한 입사각 θ 가 작다(근축광선).
(2) 각각의 광선들에 대하여 반사법칙을 적용하고
(3) 광선들의 연장선이 어디에 있게 되고 또 어디서 교차되는지를 알기 위 하여 점선으로 연장선들(허 광선들)을 그린다.
광축위에 있는 점 물체의 상점 I 는 경계에 대하여 수직인 0점을 지나는 선 분 위에 위치한다. 이 선분 즉 광학축은 구 표면의 중심C를 통과한다. 점 물 체O 로부터 광축을 따라 측정한 거울까지의 거리를 물체거리 S 라 정의하 며, 광축을 따라 상점 I 로부터 거울까지의 거리를 상거리 s' 라 한다
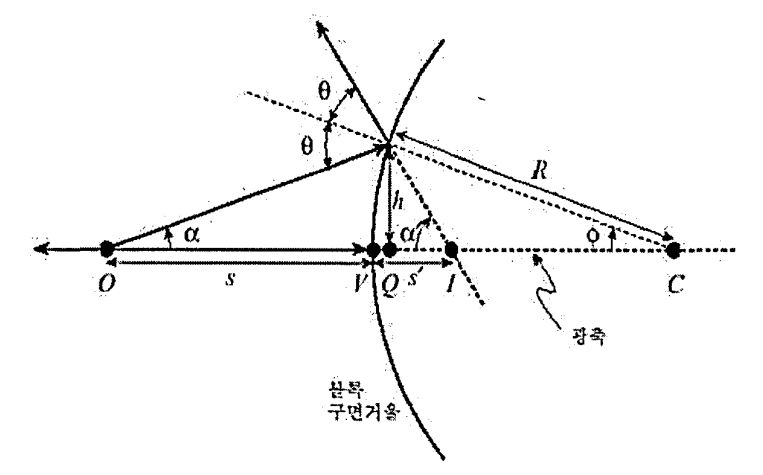
먼저 곡면의 곡률반경 R 과 물체거리 s 에 대한 상거리 s’ 의 관계를 구 해보자.
여기서는 군축광선들만으로 제한하여 전개한다.
근축광선(광축 0C에 대한)들에 대한 가정으로는 \( \alpha < \frac{\pi}{2} \) 이고, 따라서 \( \theta, \gamma, \alpha' < \frac{\pi}{2} \)이라고 하자.
이 근사는 h << R 을 의미하고, 따라서 길이 VQ는 무시한다. 삼각형의 두 내각의 합은 나머지 한 각의 외각과 같으므로
\( \theta = \alpha + \gamma \) 와 \( 2\theta = \alpha + \alpha' \)
\( \alpha - \alpha' = -2\gamma \)
각도 사이의 관계로 기술된 이 식을 거리 관계식으로 바꾸어 보자. 여기서
\( \alpha = \tan\alpha = \frac{h}{s}, \alpha' = \tan\alpha' = \frac{h}{s'}, \gamma = \tan\gamma = \frac{h}{R} \)
\( \frac{h}{s} - \frac{h}{s'} = -2\frac{h}{R} \)
이 된다. 이 식을 h로 나누면
\( 1/s - 1/s' = -2/R \)
\( 1/S + 1/S' = 2/R \)
가 되고 이 식들로 부터 S와 R을 알면 S`을 구할 수 있게 된다.
이 결과는 오목면들이나 볼록면들 둘 다에 대하여 사용 될 수 있다.
구면 거울에 대한 결상공식 : 구면 반사 경계면에 가까이 있는 물체에 대하여 물체거리 S, 상거리 S`, 거울의 골률반경 R 사이에는 다음과 같은 관계가 있다.
\( 1/S + 1/S' = 2/R \)
이 일반적인 공식은 다음과 같은 부호규약을 적용할 때 볼록 및 오목 구면 둘 다에서 적용할 수 있다.

부호 규약 :
1. 물체거리 s는 실제 물체일 경우에는 양의 값(+),허 물체일 경 우에는 음의 값(-)를 쓴다.
2. 상거리 s’는 실상일 경우 양의 값(+)으로 쓰고, 허상일 경우는 음의 값(-)으로 쓴다.
3. 곡률반경 R은 볼록면(O가 C의 반대편에 있다.) 일 경우는 양의 값 +로 쓰고, 오목면(O가 거울의 C와 같은 쪽에 있다.) 일 경우에는 음의 값(-)으로 쓴다.
이제 구면 거울에 대하여 초점거리 f 의 개념을 도입하자. 일반적으로 초점거리는 다음로 정의한다.
초점거리 : 물체점이 무한히 멀리 떨어져 있을 때 상점의 위치, 또는 이와 동등한 의미로 광학계에 평행하게 입사된 광 선들이 교차된 점까지의 거리이다.
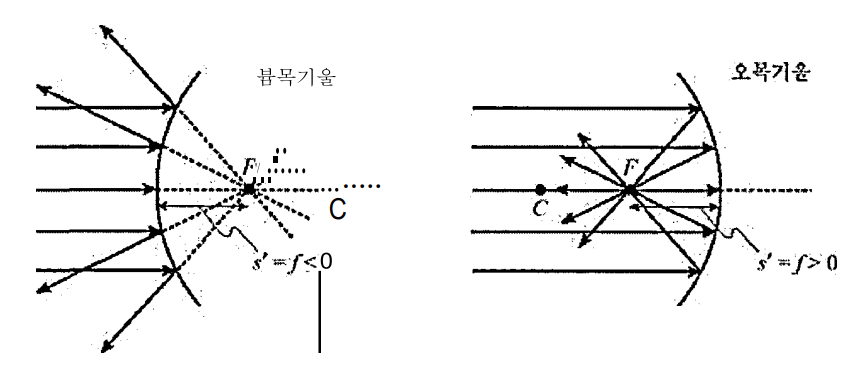
만일 구면거울에 대한 결상공식에서 S가 무한이라 하면 초점거리 f는 상거리 S`와 같다. 따라서
구면거울에 대한 결상공식은 초점거리의 항으로 다시 쓸 수 있다.
\( 1/S + 1/S' = 1/f \)
[중요] 렌즈에서도 유사 공식이 사용되며, 이 공식은 얇은 렌즈 방정식이라고 부른다.
'Optics > Ray optics' 카테고리의 다른 글
| 26. 구면거울의 시야(FOV)와 각배율 (1) | 2023.11.24 |
|---|---|
| 25. 광학 배율 (0) | 2023.11.23 |
| 23. 프리즘을 사용한 상의 방위 바꾸기 (1) | 2023.11.21 |
| 22. 평면경계를 투과한 광선의 굴절현상: 근축광선들 (1) | 2023.11.19 |
| 21. 평면 경계면에서의 반사 - 거울 (1) | 2023.11.18 |



