


여기까지는, 구면 거울 가까이에 놓여있는 단일 점 물체의 결상에 대하여 생각해 보았다.
많은 점 물체들로 구성된 더욱 복잡한 물체의 경우에는 어떻 게 될까?
한 가지 추측할 수 있는 것은 물체를 단순히 각각의 점으로 분리하 여 상을 재구성하는 것이다.
물체를 전체적으로 보게 되면 원래 물체보다 확 대된 상인가 축소된 상인가를 알 수 있다.
다음에는 배윤 m 의 개념을 도입 하자. 먼저 몇 개의 점으로 구성된 물체를 가정한다.
물체 선분의 한쪽 끝을 통하여 광축이 지나고 물체 선분은 이것에 수직이라고 하자. 앞에서는 광축 위에 있는 상의 위치를 결정했는데 여기서는 크기를 갖고 있는 물체에 대한 상의 높이를 어떻게 구하는지를 생각해 보자.
상점을 구하는 일반적 규칙을 비축(off-axis) 물체에 대하여 적용하면;
(1) 하나의 비축 물체 점으로부터 2개의 광선을 그린다. 즉, i) 한 광선은 구면 경계면에 수직으로 입사 하는 광선이고, ii) 다른 한 광선은 구면 경계와 광축의 교점에 입사한다.
(2) 각각의 광선에 대하여 반사의 법칙을 적용한다.
(3) 비축 상점의 위치를 나타내주는 광선 교차점 위치나 광선 위치를 구하기 위하여 경계에 입사된 광선 경로를 점선으로(가상 광선들) 연장한다. 그런후에 광축으로부터 측정된 상점과 비축 물체의 높이를 비교한다.
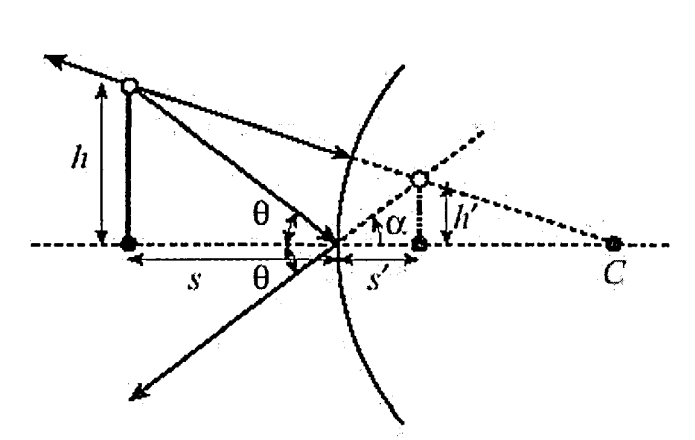
배율은 상의 크기가 물체와 비교하여 커졌는지 또는 작아졌는지를 나타내 준다. 따라서 배율은 다음으로 정의 된다.
측배율 (Lateral Magnification) : 상의 크기와 물체의 크기의 비율, 또는 \( m = \frac{h'}{h} \)
위 그림을 보면 \( \theta = \alpha \) 이므로
\( \frac{h}{s} = \tan \theta = \tan \alpha = \frac{h'}{-s'} \) (부호 규약에 의해 \(-s'\)는 양의 값을 갖는다)
따라서 배율은 물체거리와 상거리의 비로 쓸 수 있다.
배율 \( m = -\frac{S'}{S} \)
이 공식에서 사용한 (-) 부호로 인해 혼돈이 있을 수 있으나, 부호규약을 따르기 위하여 정의한 것으로 배율m 이 양의 값을 갖을 때는 상은 도립되지 않거나 위의 예에서처럼 윗 방향으로 유지하고 있는 경우이다.
그러나 m 이 음의값을 갖을 때는 상은 도립되거나 또는 광축에 대하여 뒤집힌 경우이다.
만일 사용하는 렌즈의 초점거리 f 를 알고 있고( 또는 구면 거울에 대한 곡률반경 R ), 물체거리 s 가 주어 진다면 배율 m 과 상거리 s' 는 즉각적으로 결정될 수 있다.
'Optics > Ray optics' 카테고리의 다른 글
| 27. 구면 경계면에서의 굴절 (1) | 2023.11.24 |
|---|---|
| 26. 구면거울의 시야(FOV)와 각배율 (1) | 2023.11.24 |
| 24. 구형 경계면에서의 반사 (1) | 2023.11.22 |
| 23. 프리즘을 사용한 상의 방위 바꾸기 (1) | 2023.11.21 |
| 22. 평면경계를 투과한 광선의 굴절현상: 근축광선들 (1) | 2023.11.19 |



