


굴절률이 다른 광학적 매질들 사이의 경계를 통과하는 광선들의 방향변화는 Snell의 법칙으로 기술된다.
경계로부터 어떤 거리 u 위치에 있는 점광원 으로부터 나오는 모든 광선들은 경계에 입사된 후 굴절되어 경계로부터 예측 될 수 있는 거리 u'에 점광원의 상을 형성한다.
그러면, 평면표면을 통과하는 광선들이 굴절에 의하여 실재로 점광원의 상을 형성할 수 있겠는가?
\( \tan(\alpha) = -\frac{h}{u} \)
\( \tan(\alpha') = -\frac{h}{u'} \)
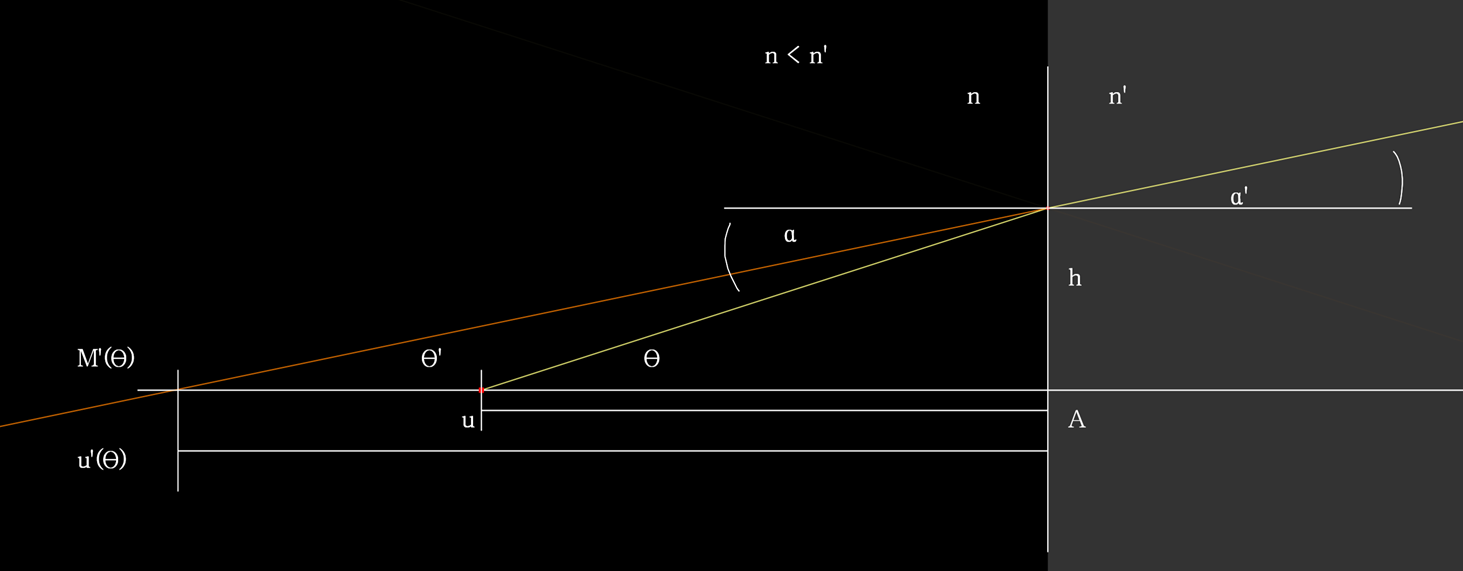
그림에서 보면 물체 M은 굴절률이 다른 두 매질의 평면 경계면의 정점 A로부터 u=AM 거리에 있다.
물체공간과 상공간의 굴절률들은 각각 n과 n'이고, n' > n 이다.
광선이 기울기 각 \( \theta \), 입사각 \( \alpha \)로, AB=h 높이의 경계면에 입사되었고,
이 광선은 Snell의 법칙에 따라 굴절되었다.
경계면에서 굴절된 광선을 그림에서처럼 점선으로 뒤로 연장하면 광축과 \( M'_\theta \)에서 교차된다.
광선의 기울기는 \( \theta' = \alpha' \)이다. 그림을 보면 상거리는 \( u'_\theta = M'_\theta \)으로 주어진다.
\( u'_\theta = \frac{\tan(\alpha)}{\tan(\alpha')} \times u \)
이 식에 따르면 상거리 \( u' \)는 굴절각과 입사각의 탄젠트의 비에 의존하는 것처럼 보인다.
그러나 광선의 기울기(또는 입사각)의 증가에 따라 굴절이 1차 함수적으로 변화되지 않으므로 이 비율은 기울기에 따라 1차적으로 변하지 않는다.
즉, 굴절된 광선은 표면으로부터의 거리의 변화에 따라 축과 교차된 거리가 변화되어 상은 한 점으로 형성되지 않는다. 이때 상은 구면적 형태의 수차를 갖는다고 말한다.
한 예로, 만일 물체가 공기(n=1) 중에 있고, 물체는 거리 u= -10cm 위치에 있고, 상이 유리(n'=1.5) 속에 만들어진다면,
\( u' \)는 \( \alpha \)값에 따라 다음과 같이 구해진다:
\( \alpha = 0 \) deg 이면 \( u'_\theta = -15 \)cm,
\( \alpha = 15 \) deg 이면 \( u'_\theta = -15.3 \)cm,
\( \alpha = 30 \) deg 이면 \( u'_\theta = -16.33 \)cm,
\( \alpha = 45 \) deg 이면 \( u'_\theta = -18.71 \)cm.
'Optics > Ray optics' 카테고리의 다른 글
| 17. 평면 표면에서의 근축 굴절 (2) (0) | 2023.11.15 |
|---|---|
| 16. 평면 표면에서의 근축 굴절 (1) (0) | 2023.11.14 |
| 14. 내부 전반사와 임계각 (1) | 2023.11.12 |
| 13. 광학적 경로길이(OPL) (1) | 2023.11.11 |
| 12. 광선 가역성의 원리 (0) | 2023.11.10 |



