


For coherent construction of the harmonic emission, the wave fronts of the fundamental laser and the generated harmonics must be in phase. Atoms along the path of the laser produce harmonics propagating with the laser field. When they are in phase with the laser wave front, there is constructive interference and these harmonics combine to build up the harmonic emission. The distance over which the fundamental wave front and the harmonic wave front become out of phase is called the coherence length and is given by
$$ L_{\text{coh}} = \frac{\pi}{\Delta k}, $$ where \(\Delta k\) is the phase mismatch.
For phase matching in the HHG process, one needs: $$ \Delta k = q k_1 - k_q = 0, $$ where \(q\) is the harmonic order, \(k_1\) is the wavevector of the \(q\)-th harmonic, and \(k_0\) is the wave vector of the fundamental beam.
In general, the wavevector \(k\) of light with wavelength \(\lambda\) propagating in a gas medium is given by: $$ k = \frac{2\pi}{\lambda} + \frac{2\pi N_a n(\lambda)}{\lambda} - N_e r_e \lambda, $$ where \(N_a\) is the atom density, \(N_e\) is the free electron density in the medium, \(n(\lambda)\) is the refractive index per unit neutral atom density at wavelength \(\lambda\), and \(r_e\) is the classical electron radius.
The intensity \(I_q\) of the \(q\)-th harmonic at the end of the nonlinear medium without absorption is given by: $$ I_q \propto L^2 \sin^2\left(\frac{\Delta k_q L}{2}\right) / \left(\Delta k_q \frac{L}{2}\right)^2, $$ where \(L\) is the length of the medium. From equation $$ k = \frac{2\pi}{\lambda} + \frac{2\pi N_a n(\lambda)}{\lambda} - N_e r_e \lambda, $$
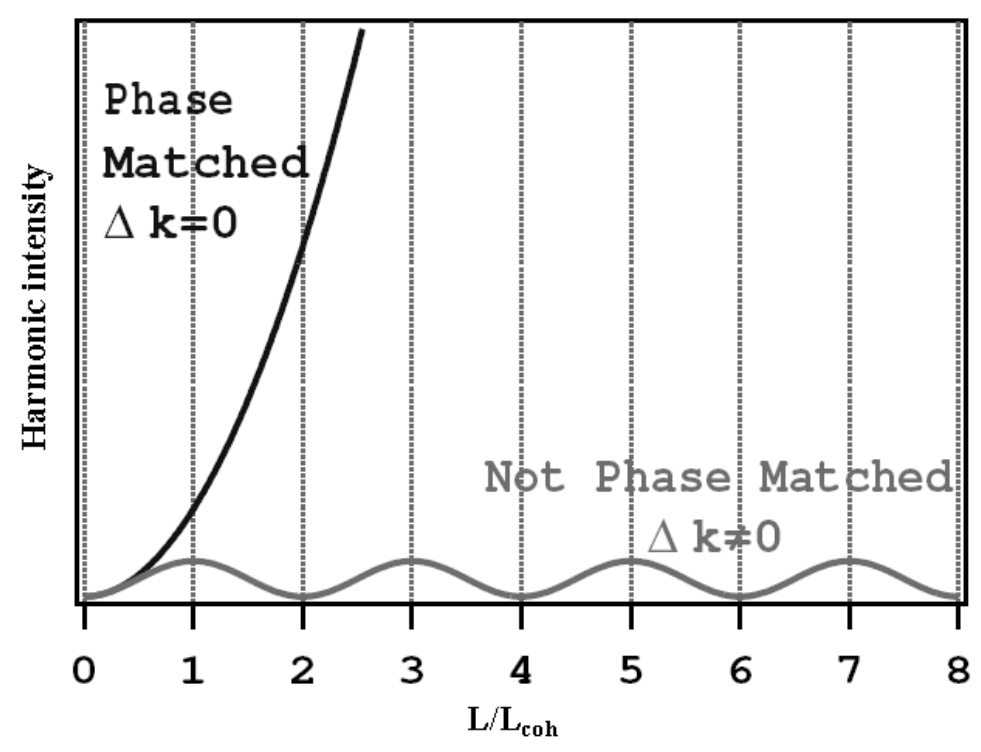
when the phase mismatch is zero, the harmonic intensity increases quadratically with the propagation distance. Otherwise, the harmonic intensity will oscillate sinusoidally with propagation distance and the periodicity of this oscillation is twice the coherence length, \(L_{\text{coh}}\).
The harmonic yield is severely limited by phase mismatch phenomena, such as the difference between the diffraction rates for the fundamental beam and the individual harmonic radiation due to geometrical propagation effects, the wavelength dependent index of refraction of the neutral atomic and ionized medium, and the dependence of the intrinsic phase of the harmonics on the laser intensity in both the longitudinal and radial directions. In general, the total phase mismatch is the sum of four terms and can be expressed as
The phase mismatch \(\Delta k_q\) is given by the equation: $$ \Delta k_q = q k_0 - k_q = \frac{2\pi q}{\lambda} p \delta n (1 - \eta) - \pi N_{\text{atm}} r_e \lambda \left(\frac{q - 1}{q}\right) + \text{(geometric term)} + \text{(atomic phase)}, $$ where \(\lambda\) is the laser wavelength; \(p\) and \(\eta\) are the gas pressure and ionization fraction, respectively; \(\delta n = n_{\text{laser}} - n_q\), \(n_{\text{laser}}\) and \(n_q\) are the refractive indices for the laser light and the \(q\)-th harmonic, respectively, and \(N_{\text{atm}}\) is the atomic number density at 1 atm.
In this expression for the phase mismatch the first (positive) term is related to the medium dispersion and the second (negative) term is due to the plasma dispersion. The geometric term is negative in a waveguide or self guide. For a focused Gaussian beam the geometrical phase shift around the focal point is due to the Gouy phase shift. The sign of the atomic dipole phase term is not fixed since this phase varies with the intensity of the laser field.
Geometrical Phase Mismatch
This phase mismatch arises primarily from the Gouy phase shift when the laser beam is focused. For a Gaussian beam, the Gouy shift can lead to a phase deviation between the laser wave front passing through the focus and the phase front of a plane wave with the same optical frequency, and is given by: $$ \Phi_{\text{Gouy}}(z) = \tan^{-1}\left(\frac{z}{Z_R}\right), $$ where \(Z_R = \frac{\pi w_0^2}{\lambda}\) is the laser Rayleigh length, \(w_0\) is the beam waist radius (for a typical f/50 geometry with 800 nm wavelength, \(Z_R = \frac{\pi w_0^2}{\lambda} = 2.5 \, \text{mm}\)), and \(z\) is the distance from the beam focus along the axis of propagation.
As a consequence, the phase for the \(q\)-th harmonic order at each point where it is generated along the \(z\) direction is: $$ \Phi_{\text{Gouy}, q} = q \Phi_{\text{Gouy}} = q \tan^{-1}\left(\frac{z}{Z_R}\right). $$
The Gouy shift for the harmonics themselves as they propagate along the \(z\) direction can be neglected compared to the Gouy shift shown in the equation above.
If we define the distance over which the phase given by the above equation shifts by \(\pi\) as the coherence length relating to the Gouy shift, we can estimate this distance.
This coherence length can be calculated by taking the derivative of the phase and setting it equal to \( \pi \): $$ \frac{d\Phi}{dz} = \frac{q}{\frac{Z_R^2 + \left(\frac{z}{Z_R}\right)^2}{Z_R}} \approx \frac{q}{\frac{Z_R^2 + z^2}{Z_R}} $$
Then, this coherence length is given by: $$ L_{\text{coh,G}}(z) = \frac{\pi \left(Z_R + \frac{z^2}{Z_R}\right)}{q} $$
Close to the centre of the beam focus (\( z \approx 0 \)), \( L_{\text{coh,G}} \) may be rewritten as: $$ L_{\text{coh,G}}(z) = \frac{\pi Z_R}{q} $$
For a typical f/50 geometry with 800 nm wavelength, the Gouy coherence length near the centre of the focus can be estimated to be 0.32 mm for the harmonic H25. According to equation about \( L_{\text{coh,G}}(z) \) is larger when \( z \) is longer, i.e., the Gouy phase related coherence length is longer at positions away from the focus.
The contribution from the Gouy phase can be controlled by placing the focus at a different position with respect to the gas medium. When the laser is focused before the generating medium, phase matching on the optical axis is efficient leading to spatial and spectral harmonics that are regular. When the focus is at the centre of the medium, the harmonic intensity is low owing to poor phase matching. On the other hand, when the laser is focused after the medium, efficient phase matching is achieved for off-axis emission, resulting in a high conversion efficiency but distorted spatial and temporal profiles.
Neutral Gas Dispersion Phase Mismatch
This phase mismatch contribution is due to material dispersion and is given by (for harmonic q)
The phase mismatch for harmonic generation is given by: $$ \Delta k_N = \frac{2\pi q}{\lambda} (n_{\text{laser}} - n_{\text{harmonic}}) $$
We define \(\delta n = n_{\text{laser}} - n_{\text{harmonic}}\) as the difference of the refraction index of the gas per unit atmosphere at the fundamental and harmonic wavelengths. The refractive indices of the noble gases are close to unity and depend on the frequency. For a fundamental wavelength \(\lambda = 800 \text{ nm}\), \(n(\lambda) \approx 1 + 2.8 \times 10^{-4}\), and for harmonics \(q > 21\), \(n(\lambda_q) \approx (1-10^{-4}) - (1-10^{-6})\) at STP (1 atm and 273K), where \(\lambda_q\) is the wavelength of the \(q\)-th harmonic.
The refractive index is proportional to the gas pressure (in atm) and when the gas medium is ionized the fraction of ionization is usually given by \(\eta = \frac{N_e}{N_a}\), where \(N_e\) and \(N_a\) are electron and atomic number density respectively. Therefore, we can be rewritten as: $$ \Delta k_N = \frac{2\pi q}{\lambda} p \delta n(1-\eta) $$
For low ionization level \(\eta \ll 1\).
For a gas pressure of 50 Torr, and assuming the ionization fraction in the medium is 1%, the neutral dispersion phase mismatch for harmonic H25 is found to be around 45 cm\(^{-1}\).
It is worth recalling that when a laser with high intensity propagates through a medium, this also causes a change in the refractive index in proportion to the laser intensity. This change is known as the instantaneous change and given as: $$ \Delta n = n_2 I(t) $$ where \(n_2\) is the nonlinear refractive index.
Plasma Dispersion Phase Mismatch
When an intense laser beam interacts with a gas medium, not only harmonics but also free electrons are emitted during the ionization process. The free electrons cause plasma dispersion which can reduce the coherencelength, i.e., limit the harmonic yield. The refractive index for a plasma is given by
The plasma refractive index \( n_p(\omega_0) \) is given by: $$ n_p(\omega_0) = \sqrt{1 - \frac{\omega_p^2}{\omega_0^2}} $$ where \( \omega_0 \) is the laser frequency, and \( \omega_p \) is the plasma frequency, given by: $$ \omega_p = e \sqrt{\frac{N_e}{\epsilon_0 m_e}} $$ Here, \( N_e \) is the density of free electrons, \( \epsilon_0 \) is the vacuum permittivity, and \( m_e \) is the electron mass.
Since \( \omega_0 \) is much larger than \( \omega_p \), i.e., \( \omega_p^2 \ll \omega_0^2 \), then it can be rewritten as: $$ n_p(\omega_0) \approx 1 - \frac{\omega_p^2}{2\omega_0^2} $$
If we define \( L_{\text{coh, p}} \) as the coherence length relating to the plasma dispersion, it can be calculated from: $$ L_{\text{coh, p}}(qk_0 - k_q) = \frac{2\pi q}{\lambda_0} \left( n_p(\omega_0) - n_p(q\omega_0) \right) L_{\text{coh, p}} = \pi $$ Then, \( L_{\text{coh, p}} \) is given by: $$ L_{\text{coh, p}} = \frac{4\pi^2 m_e}{N_e e^2 \mu_0 \lambda_0 (q - 1/q)} $$
Where \( \mu_0 = \frac{1}{c^2 \epsilon_0} \) is the vacuum permittivity.
If we assume \( q \gg 1 \), then equation is given approximately by: $$ L_{\text{coh, p}} = \frac{4\pi^2 m_e}{N_e e^2 \lambda_0 \mu_0 q} $$
we can see that the coherence length scales inversely with the harmonic order. To produce a higher order harmonic, a higher intensity of the fundamental beam needs to be applied. This leads to an increase of the ionization rate and free electron density. Therefore, the plasma phase mismatch becomes more important with increased harmonic order.
Also, equation indicates that the coherence length decreases as the free electron density increases.
If we assume a linear dependence between the density of the generating medium and the free electron density, this suggests that increasing the gas pressure does not merely lead to a higher harmonic yield. For example, for a gas pressure of 50 Torr, and if we assume that one electron per atom is ionized and there is complete ionization in the medium, the coherence length can be calculated to be approximately 37 μm for harmonic H25 and becomes two times shorter if the gas pressure is increased up to 100 Torr.
The phase mismatch due to plasma dispersion is given by: $$ \Delta k_p = \frac{\pi}{L_{\text{coh, p}}} = - \frac{N_e e^2 \mu_0 (q - \frac{1}{q})}{4\pi m_e} $$
Moreover, the classical electron radius is given by: $$ r_e = \frac{1}{4\pi \epsilon_0} \frac{e^2}{m_e c^2} $$
The electron density can be expressed as: $$ N_e = \eta N_{\text{atm}} $$
The phase mismatch due to the plasma dispersion is: $$ \Delta k_p = \eta N_{\text{atm}} r_e \lambda_0 \left(q - \frac{1}{q}\right) $$
Using the same conditions which give a coherence length of 37 μm, the plasma phase mismatch of harmonic H25 for complete ionization is about 850 cm^{-1}. This phase mismatch is one hundred times smaller, i.e., 8.5 cm^{-1}, if the ionization fraction in the medium is 1%.
The contribution from the phase mismatch due to neutral gas dispersion is positive and that due to plasma dispersion is negative. This allows us to reduce the total phase mismatch by varying the laser intensity to adjust the fraction of ionization. However, one must consider the critical value of the ionization fraction, \( \eta_{\text{cr}} \). At this value, the dispersion from the remaining neutral atoms is not enough to balance the dispersion from the free electrons.
To obtain phase matching in high harmonic generation, the ionization fraction must be lower than a critical ionization fraction.
The critical value can be expressed as: $$ \eta_{\text{cr}} = \left[1 + \frac{N_{\text{atm}} r_e \lambda^2}{2\pi (\delta n)}\right]^{-1} $$
We find that the critical ionization is independent of the pressure. In the case of no compensation of the phase mismatch, this equation allows us to estimate the limiting value of the ionization fraction in the medium in order for phase matching to be achieved. Typical values of \( \eta_{\text{cr}} \) for common gases at 800 nm wavelength are quite low, about 0.5% in He, 1% in Ne and 5% in Ar. These critical values limit the phase matched highest order harmonics that can be achieved by simply tuning the pressure: H91, H69, H35 in He, Ne, and Ar, respectively. In order to overcome this limitation, alternative approaches need to be used.
Atomic Dipole Phase Mismatch
Theorigin of this phase is the trajectory acquired by the electron leading to the emission of the qth harmonic in the continuum state. To a first approximation, the phase of the atomic dipole varies linearly with the laser intensity. The laser intensity can vary spatially in both the longitudinal and radial directions. Therefore, the atom dipole phase also varies axially as well as radially. This leads to reduced harmonic emission as well as strong spatial distortion. It may be possible to find situations in which the intrinsic phase can be played against the geometrical phase mismatch in order to improve overall phase matching.
For example, in the simple case when the contribution of the Gouy phase shift and dipole phase are considered, the phase mismatch will be minimal when the variation of the harmonic phase with propagation is minimal. When the laser confocal parameter is equal to 5 mm and the focus position is located at z = 0, P. Salières et al. find that when the laser is focused approximately 3 mm before the generating medium, the harmonic phase variation is minimal, i.e., the phase mismatch is a minimum.
For a Gaussian laser beam with intensity along the direction of propagation
The intensity profile \( I(z) \) along the z-axis of the beam is given by: $$ I(z) = \frac{I_0}{1 + \left(\frac{2z}{b}\right)^2} $$ where \( I_0 \) is the peak intensity and \( b \) is the Rayleigh length.
The contribution of the dipole phase to the phase mismatch on the axis of the \(q\)-th harmonic, \(V_{\phi_q}\), is given by: $$ V_{\phi_q} = -\alpha_q \frac{\partial I}{\partial z} = -\frac{8z \alpha_q I_0}{b^2 \left[1 + \left(\frac{2z}{b}\right)^2\right]^2} $$ where \( \alpha_q \) is a coefficient related to the electron trajectories.
Values for \( \alpha_q \) are typically \(1-5 \times 10^{-14} \text{ cm}^2/\text{W}\) for the short trajectory and \(20-25 \times 10^{-14} \text{ cm}^2/\text{W}\) for the long trajectory, and \( b \) is the Rayleigh length.
This dependence of the laser field amplitude and phase on the propagation clearly shows that the dipole phase cannot be established assuming an unperturbed laser beam. In a long interaction length geometry, e.g., a semi-infinite cell, the dipole phase cannot be neglected and the phase gradient of the dipole phase allows the phase mismatch on axis to be reduced in the region where the laser intensity is high.
This leads to an enhancement of the high harmonic generation (HHG) efficiency because the atomic response is high. The atomic dipole phase gradient acts as an additional time-dependent wave vector which allows a high plasma dispersion to be compensated.
'Optics > Miscellaneous' 카테고리의 다른 글
| 11. HHG Spectrum and Strong Field Approximation (SFA) Model (0) | 2024.05.07 |
|---|---|
| 10. Principles of High Harmonic Generation (0) | 2024.05.02 |
| 9. Rayleigh-Sommerfeld Diffraction (0) | 2024.04.11 |
| 8. ABCD Matrix을 이용한 Ray tracing 계산 (0) | 2024.04.08 |
| 7. 포토공정(Photolitho)에서 Aberration(수차)의 영향성 (0) | 2024.03.28 |



