


https://arxiv.org/pdf/1812.11447
위 링크의 정보 참고하시면 좋을 것 같습니다.
As mentioned in the three step model, at one half-cycle after ionization, the electron turns back towards the parent ion to recombine when the laser electric field changes sign. Hence, the harmonics are produced twice each cycle and each half cycle of the driving laser produces a short (subfemtosecond) burst of XUV radiation. Thus, the harmonics are characterized by a series of bursts in the time domain separated by half the laser period.
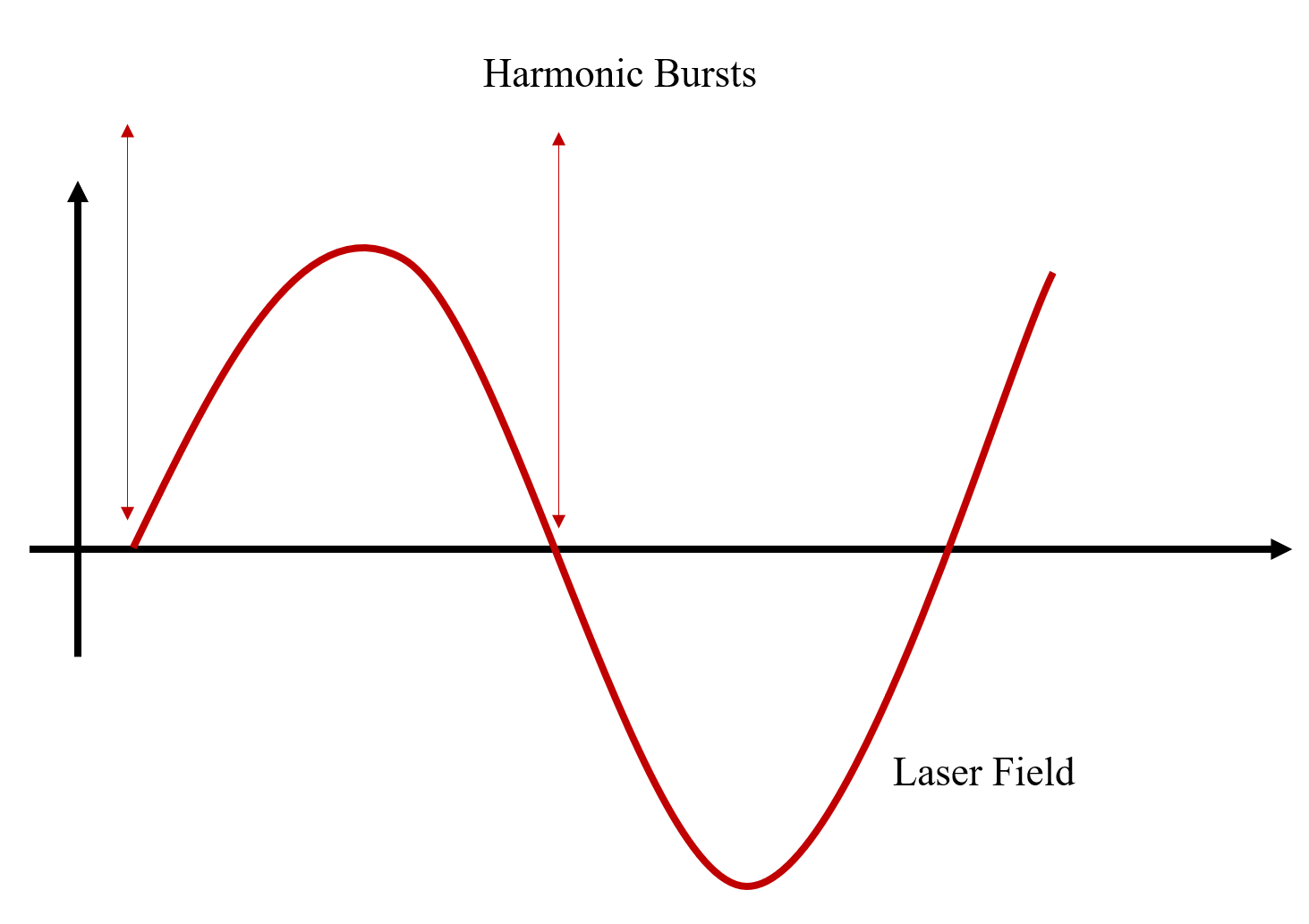
By taking a Fourier transform, this separation of half the laser period in the time domain results in peaks separated by \(2\omega_0\) in the frequency domain. In addition, since the consecutive bursts are a consequence of collisions from opposite directions, the corresponding spectral components have the same amplitude but opposite in phase. This leads to destructive spectral interference for even order harmonics \(\omega = 2m\omega_0\), and constructive interference for odd harmonics \(\omega = (2m+1)\omega_0\). This is why, normally, only odd harmonics are observed in the HHG spectrum.
A typical HHG spectrum can be divided into three parts: the perturbative region at low orders, the plateau region at intermediate orders, and the cutoff region at highest orders. Perturbation theory can be used to describe the appearance of lower order harmonics \(q < 9\) which are produced at low intensities during the leading edge or trailing edge of the laser pulse. Basically, the harmonic yields in this region decrease as a power law.
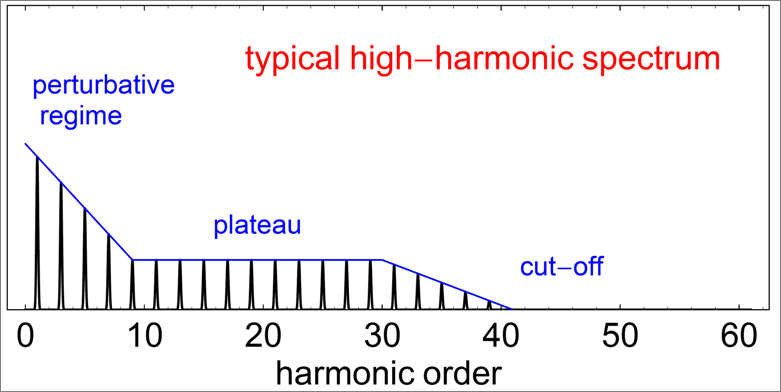
The higher order harmonics are generated at higher laser intensities. When the electric field strength of the laser is on the same scale as the inner atomic electric fields, it cannot be considered as a small perturbation anymore, i.e., perturbation theory breaks down.
The plateau region contains the harmonics which are produced when applying a high strength driving electric field. In this region, the harmonic intensities are relatively unchanged with increasing order. Another interesting point is that, in the plateau region, two electron trajectories contribute to the harmonic spectrum.
Electrons in these two trajectories are ionized at different phases of the laser field. However, they can return to the core with the same velocity, i.e., the same final kinetic energy at recombination, leading to the emission of radiation at the same frequency.
An electron on the long trajectory which is ionized at a phase of 30 returns to the parent ion close to one period of an optical cycle while an electron on the short trajectory which is produced at a phase of 450 has a return time less than half an optical cycle. The plateau region is followed by the cutoff region. The cutoff photon energy is determined by the maximum energy the recombining electron can obtain in the electric field given by blow equation.
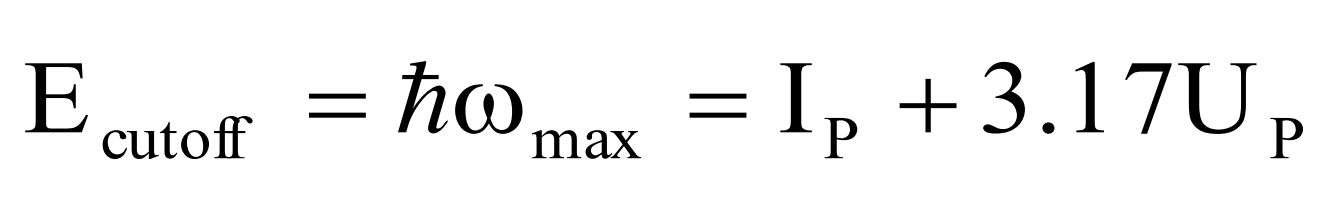
This occurs for an electron which is ionized at a phase of the laser field of 170 and therefore the maximum kinetic energy of 3.17Up is achieved.
The three step model provides the basic picture of the HHG process and has been successful in explaining the experimental observations, like the prediction of the cutoff region. However, it fails to explain the spectral characteristics of the plateau region. To deal with this problem, and to understand the HHG process more precisely, a fully quantum mechanical theory has been developed within the strong field approximation by Lewenstein et al. In this model, Lewenstein et al. solved numerically the time dependent Schrödinger equation in a strong field with the assumptions:
- The contribution to the wave packet of all bound states except the ground state can be neglected
- There is no depletion of the ground state
- In the continuum states, the electron can be treated as a free particle moving in the electric field with no effect of the atomic potential
Lewenstein et al. claimed that an electron is promoted into a continuum state by the laser field, then propagates in the laser field, and finally recombines with the parent ion by a dipole transition.
In addition, in the SFA approach, calculation of the harmonic dipole moment is performed as the coherent sum of all the different quantum paths which contribute to the harmonic emission. The phase associated with each quantum path is given by the classical action accumulated by the electron along the corresponding trajectory and can be approximated by the product of the ponderomative energy and the electron excursion time.
Based on the SFA model, it is shown that the phase of the dipole moment depends on the laser intensity.
This leads to an intensity dependent harmonic phase which helps us to explain successfully different aspects of the generation process. Also, the Lewenstein model predicts a cutoff energy, $$ E_{\text{cutoff}} = \hbar \omega_{\text{max}} = F I_p + 3.17 U_p, $$ slightly higher than that in the three step model. The factor \( F(I_p / U_p) \) is equal to \( I_p \ll U_p \) and approaches unity as \( I_p \) grows.
'Optics > Miscellaneous' 카테고리의 다른 글
| 12. Phase Matching in High Harmonic Generation (HHG) (0) | 2024.05.09 |
|---|---|
| 10. Principles of High Harmonic Generation (0) | 2024.05.02 |
| 9. Rayleigh-Sommerfeld Diffraction (0) | 2024.04.11 |
| 8. ABCD Matrix을 이용한 Ray tracing 계산 (0) | 2024.04.08 |
| 7. 포토공정(Photolitho)에서 Aberration(수차)의 영향성 (0) | 2024.03.28 |



