9. Rayleigh-Sommerfeld Diffraction

 

Another method to propagate a wave field is by using the Rayleigh-Sommerfeld integral. A very good approximation of this integral states that each point in the plane  z=0 emits spherical waves, and to find the field in a point  (x,y,z)
 , we have to add the contributions from all these point sources together. 

This corresponds to the Huygens-Fresnel principle postulated earlier in Section 5.6. Because a more rigorous derivation starting from the Helmholtz equation would be complicated and lengthy, we will just give the final result:

 

$$\begin{array}{rl}U(x,y,z)& =\frac{1}{i\mathrm{\lambda <!--\; \lambda \; -->}}\iint <!--\; \iint \; -->U(x^{\mathrm{\prime <!--\; \prime \; -->}},y^{\mathrm{\prime <!--\; \prime \; -->}},0)\frac{z{e}^{ik\sqrt{{(x-<!--\; -\; -->x^{\mathrm{\prime <!--\; \prime \; -->}})}^2+{(y-<!--\; -\; -->y^{\mathrm{\prime <!--\; \prime \; -->}})}^2+z^2}}}{{(x-<!--\; -\; -->x^{\mathrm{\prime <!--\; \prime \; -->}})}^2+{(y-<!--\; -\; -->y^{\mathrm{\prime <!--\; \prime \; -->}})}^2+z^2}\mathrm{d}{x}^{\mathrm{\prime <!--\; \prime \; -->}}\mathrm{d}{y}^{\mathrm{\prime <!--\; \prime \; -->}}\\ & =\frac{1}{i\mathrm{\lambda <!--\; \lambda \; -->}}\iint <!--\; \iint \; -->U(x^{\mathrm{\prime <!--\; \prime \; -->}},y^{\mathrm{\prime <!--\; \prime \; -->}},0)\frac{z{e}^{ikr}}{r}\mathrm{d}{x}^{\mathrm{\prime <!--\; \prime \; -->}}\mathrm{d}{y}^{\mathrm{\prime <!--\; \prime \; -->}}\end{array}$$

 

where we defined

 

 

$$r=\sqrt{{(x-<!--\; -\; -->x^{\mathrm{\prime <!--\; \prime \; -->}})}^2+{(y-<!--\; -\; -->y^{\mathrm{\prime <!--\; \prime \; -->}})}^2+z^2}.$$

 

 

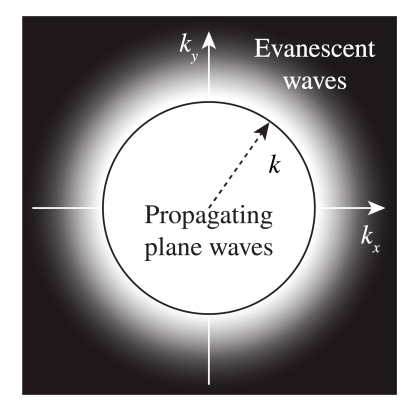
The spatial frequencies \(k_x, k_y\) of the plane waves in the angular spectrum of a time-harmonic field which propagates in the \(z\)-direction. There are two types of waves: the propagating waves with spatial frequencies inside the circle: \(\sqrt{k^2_x + k^2_y} < k = \frac{2\pi}{\lambda}\) and which have phase depending on the propagation distance \(z\) but constant amplitude, and the evanescent waves for which \(\sqrt{k^2_x + k^2_y} > k\) and of which the amplitude decreases exponentially during propagation.