


High harmonic generation - Wikipedia
From Wikipedia, the free encyclopedia Laser science process High-harmonic generation (HHG) is a non-linear process during which a target (gas, plasma, solid or liquid sample) is illuminated by an intense laser pulse. Under such conditions, the sample will
en.wikipedia.org
이 글에 대한 백그라운드 설명은 상기 위키디피아 링크를 참조해주세요.
This is opposite to traditional optics theory in which a linear relationship between the low applied electric field \( E \) of light and the dielectric polarization \( P \) of a material is given by
\[ P = \epsilon_0 \chi E \quad \]
where \( \chi \) is the linear susceptibility and \( \epsilon_0 \) is the permittivity.
However, at strong electric fields (up to \( 10^8 \, \text{V/m} \)), i.e., when the laser field becomes comparable to the internal atomic Coulomb field, the nonlinear terms in the induced polarization become important. The polarization can be expressed by the Taylor series:
\[ P = \epsilon_0\chi E + \epsilon_0\chi^{(2)} E^2 + \epsilon_0\chi^{(3)} E^3 + \ldots \quad \]
The first term defines the linear susceptibility, the second term defines the lowest order nonlinear susceptibility, and so on. The optical nonlinearities are small compared with the first term. When a very strong laser field is applied, a very high order of the polarization is induced. Under certain conditions, the nonlinear polarization can act as a source for the generation of frequency up-conversion of the fundamental field.
High Harmonic Generation is an extreme nonlinear optical process which occurs in the strong field regime. The required focused intensity of the fundamental beam for this process is at least \( 10^{13} \, \text{W/cm}^2 \) and can be obtained by focusing a high power femtosecond laser beam. At this laser intensity, the contribution of very high order nonlinearities becomes significant.
However, it is worth noting that there is an upper limit of laser intensity for HHG. This is related to optical breakdown when the plasma electron density reaches a critical density and becomes opaque to the pumping laser radiation. In addition, at an intensity around \( 10^{16} \, \text{W/cm}^2 \), the increased magnetic field prevents recombination with the parent atom, which suppresses the HHG process. Self-focusing of the laser beam and the creation of plasma are also limiting factors at high intensity.
Depending on the medium, such as a gas of atoms, molecules, or a solid material, the necessary focused intensities are different, and the response of the medium to the laser field is also different.
To describe accurately the HHG process, the fully numerical solution of the timedependent Schrödinger equation (TDSE) needs to be calculated.
However, a quasi classical three step model can clearly provide a physical picture of the interaction between atoms and strong laser fields and can be used to predict the features of HHG.
In this model, under the interaction of a strong laser field, the active electrons first tunnel through the potential barrier, are then accelerated, and when the laser field changes sign the accelerated electrons are pulled back and finally recombine with parent ions to emit highenergy photons.
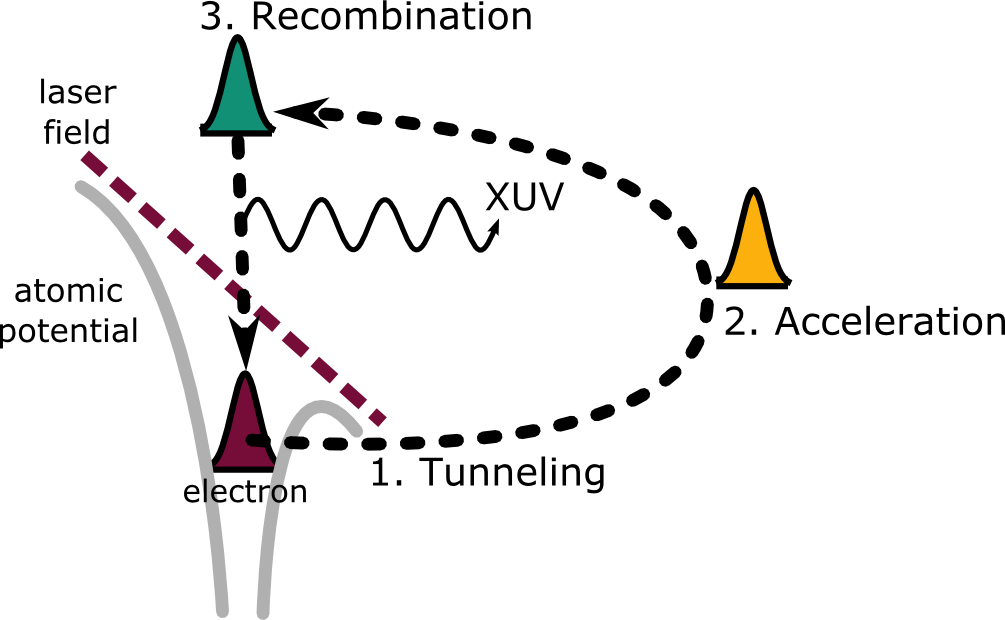
[1] In the first step, the intense laser field modifies the Coulomb potential of the atom, allowing the electron to tunnel through the barrier and ionize.
[2] After the tunnelling process, the electron is considered as a “free particle” in the electric field. The free electron accelerates in the laser field and gains momentum.
[3] When the field reverses, the electron is accelerated back toward the ionic parent. If recombination occurs, the electron releases a photon with very high energy.
The fraction of ionization in the tunnelling regime was first studied by Ammosov, Delone and Krainov (ADK model).
The rate of ionization from the ground state can be expressed as
$$ \omega(t) = \omega_p |C_n|^2 \left(\frac{4 \omega_p}{\omega_t}\right)^{2n^*-1} \exp \left(-\frac{4 \omega_p}{3 \omega_t}\right) $$ where $$ \omega_p = \frac{I_p}{\hbar}, \quad \omega_t = \left(\frac{e E(t)}{2 m_e I_p}\right)^{1/2} $$ $$ n^* = Z^* \left(\frac{I_H}{I_p}\right)^{1/2}, \quad |C_n|^2 = \frac{1}{2^{2n^*} n^* \Gamma(n^* + 1) \Gamma(n^*)} $$
In which \( I_p \) is the ionization potential of the atom, \( I_H \) is the ionization potential of atomic hydrogen, \( E(t) \) is the electric field of the laser, \( m \) is the electron mass, \( Z \) is the ion charge after ionization, and \( \Gamma \) is the Gamma function.
The fraction of ionization is given by: $$ n(t) = \exp \left( -\int_{-\infty}^{t} \omega(t') \, dt' \right) $$
During the second step, the electron gains mean kinetic energy known as the ponderomotive energy \( U_p \). This energy is directly proportional to the intensity \( I \) of the incident laser and the square of the fundamental wavelength \( \lambda \). It is given by: $$ U_p = \frac{e^2 E^2}{4m_e \omega_0^2} = \frac{e^2 I}{2m_e \omega_0^2 c \epsilon_0} \propto I \lambda^2 $$
Where \( e \) is the electron charge, \( E \) is the electric field and \( \omega_0 \) is the angular frequency of the driving laser, respectively.
When the electron returns to its parent ion, the recollision energy is not only the kinetic energy (\( U_p \)) but also the ionization potential of the atom (\( I_p \)). Thus, according to this model, the maximum energy (cutoff energy) is given by: $$ E_{\text{cutoff}} = \hbar \omega_{\text{max}} = I_p + 3.17 U_p $$
Where \( \omega_{\text{max}} \) is the maximum angular frequency and \( \hbar \) is the reduced Planck constant.
We know that \( \omega_{\text{max}} = q_{\text{max}} \omega_0 \), where \( q_{\text{max}} \) is the cutoff harmonic order. Hence, the cutoff harmonic order is: $$ q_{\text{max}} = \frac{I_p + 3.17U_p}{\hbar \omega_0} $$
The term 3.17\( U_p \) is the maximum kinetic energy upon the electron returning to the nucleus and this happens for the phase of the electric field at the instant of ionization, \( \phi \approx 17^\circ \), which is close to the maximum of the electric field.
According to equation , the cutoff can be extended by increasing the ponderomotive energy, \( U_p \). This can be achieved by using a longer wavelength of the fundamental laser or a higher laser intensity. In addition, based on equation, the extension of the position of the cutoff is also possible by using atoms with high ionization potentials, \( I_p \), like the noble gases. For example, if a fundamental beam with wavelength of 800 nm and duration of 26 fs is applied, the maximum harmonic orders that can be generated in the noble gases are H27, H41, H61, H155, H221 for Xe, Kr, Ar, Ne, and He, respectively.
'Optics > Miscellaneous' 카테고리의 다른 글
| 12. Phase Matching in High Harmonic Generation (HHG) (0) | 2024.05.09 |
|---|---|
| 11. HHG Spectrum and Strong Field Approximation (SFA) Model (0) | 2024.05.07 |
| 9. Rayleigh-Sommerfeld Diffraction (0) | 2024.04.11 |
| 8. ABCD Matrix을 이용한 Ray tracing 계산 (0) | 2024.04.08 |
| 7. 포토공정(Photolitho)에서 Aberration(수차)의 영향성 (0) | 2024.03.28 |



