


Ray transfer matrix analysis (also known as ABCD matrix analysis) is a mathematical form for performing ray tracing calculations in sufficiently simple problems which can be solved considering only paraxial rays.
Each optical element (surface, interface, mirror, or beam travel) is described by a 2×2 ray transfer matrix which operates on a vector describing an incoming light ray to calculate the outgoing ray.
Multiplication of the successive matrices thus yields a concise ray transfer matrix describing the entire optical system.
The same mathematics is also used in accelerator physics to track particles through the magnet installations of a particle accelerator, see electron optics.
This technique, as described below, is derived using the paraxial approximation, which requires that all ray directions (directions normal to the wavefronts) are at small angles θ relative to the optical axis of the system, such that the approximation sin θ ≈θ remains valid.
A small θ further implies that the transverse extent of the ray bundles (x and y) is small compared to the length of the optical system (thus "paraxial"). Since a decent imaging system where this is not the case for all rays must still focus the paraxial rays correctly, this matrix method will properly describe the positions of focal planes and magnifications, however aberrations still need to be evaluated using full ray-tracing techniques.
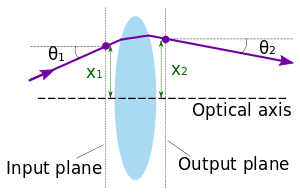
The ray tracing technique is based on two reference planes, called the input and output planes, each perpendicular to the optical axis of the system. At any point along the optical train an optical axis is defined corresponding to a central ray; that central ray is propagated to define the optical axis further in the optical train which need not be in the same physical direction (such as when bent by a prism or mirror).
The transverse directions x and y (below we only consider the x direction) are then defined to be orthogonal to the optical axes applying. A light ray enters a component crossing its input plane at a distance x1 from the optical axis, traveling in a direction that makes an angle θ1 with the optical axis.
After propagation to the output plane that ray is found at a distance x2 from the optical axis and at an angle θ2 with respect to it. n1 and n2 are the indices of refraction of the media in the input and output plane, respectively.
The ABCD matrix representing a component or system relates the output ray to the input according to
where the values of the 4 matrix elements are thus given by
and
This relates the ray vectors at the input and output planes by the ray transfer matrix (RTM) M, which represents the optical component or system present between the two reference planes. A thermodynamics argument based on the blackbody radiation [citation needed] can be used to show that the determinant of a RTM is the ratio of the indices of refraction:
As a result, if the input and output planes are located within the same medium, or within two different media which happen to have identical indices of refraction, then the determinant of M is simply equal to 1.
A different convention[2] for the ray vectors can be employed. Instead of using θ≈sin θ, the second element of the ray vector is n sin θ, which is proportional not to the ray angle per se but to the transverse component of the wave vector. This alters the ABCD matrices given in the table below where refraction at an interface is involved.
The use of transfer matrices in this manner parallels the 2×2 matrices describing electronic two-port networks, particularly various so-called ABCD matrices which can similarly be multiplied to solve for cascaded systems.
That's it for the brief explanation. Let's take a look at the lens equation example to see how it works. If you've forgotten about the lens equation or want a refresher, here's a link to it.
https://namu.wiki/w/%EC%96%87%EC%9D%80%20%EB%A0%8C%EC%A6%88%20%EB%B0%A9%EC%A0%95%EC%8B%9D
얇은 렌즈 방정식
thin-lens equation 얇은 렌즈 의 상 거리, 물체 거리, 초점 거리 간의 관계를 담은 방정식이다.
namu.wiki
Example : Thin lens
Consider a beam traveling through a thin lens with focal length f. The ray transfer matrix is
and so
Only the real part of 1/q is affected: the wavefront curvature 1/R is reduced by the power of the lens 1/f, while the lateral beam size w remains unchanged upon exiting the thin lens.
f = focal length of lens where f > 0 for convex/positive (converging) lens.
Only valid if the focal length is much greater than the thickness of the lens.
Methods using transfer matrices of higher dimensionality, that is 3×3, 4×4, and 6×6, are also used in optical analysis.
In particular, 4×4 propagation matrices are used in the design and analysis of prism sequences for pulse compression in femtosecond lasers.
Example : Think lens
n1 = refractive index outside of the lens.
n2 = refractive index of the lens itself (inside the lens).
R1 = Radius of curvature of First surface.
R2 = Radius of curvature of Second surface.
t = center thickness of lens.
By applying this method, you can calculate a customised full optical system and get the desired results.
'Optics > Miscellaneous' 카테고리의 다른 글
| 10. Principles of High Harmonic Generation (0) | 2024.05.02 |
|---|---|
| 9. Rayleigh-Sommerfeld Diffraction (0) | 2024.04.11 |
| 7. 포토공정(Photolitho)에서 Aberration(수차)의 영향성 (0) | 2024.03.28 |
| 6. What is light? (0) | 2024.03.19 |
| 5. Laser Spot Size Calculator, 레이저 초점 크기 계산기 (1) | 2023.12.26 |











