


4준위 레이저
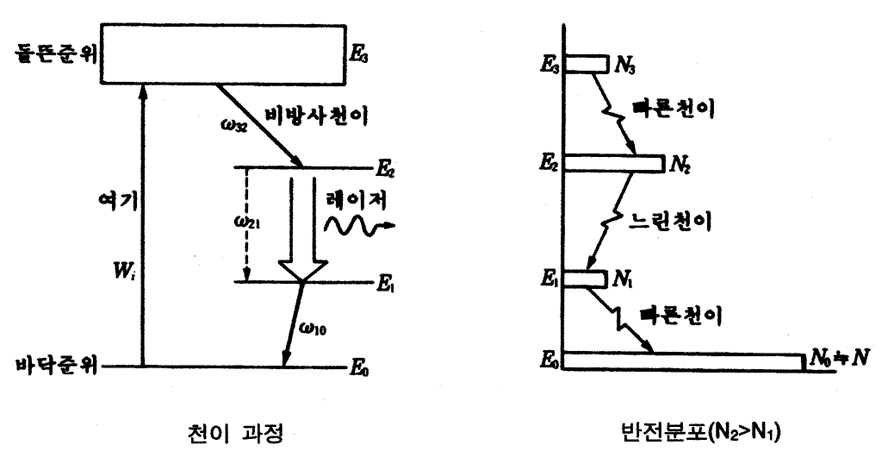
반전분포를 실현시키면 레이저 증폭작용이 일어나는 것은 당연하다고 할 수 있다. 문제는 어떻게 입자수분포를 반전시키는가 하는 것이다. 실제 레이저에서 잘 이용되는 것은 3준위계 또는 4준위계의 완화 시간차를 이용하는 방법이다.
우측의 그림은 이상적인 3준위 레이저의 에너지준위를 나타낸 것이다. 레이저의 경우, 각 준위 사이에 생기는 에너지차는 열에너지에 비해 아주 크기 때문에 열평형상태에서 거의 모든 원자는 바닥준위인 준위 1에 있다.
이와 같은 원자의 집단에 외부에서 ν31=(E3-E1)∕h에 가까운 주파수의 강력한 광을 입사시켜 바닥준위의 원자를 준위 3으로 여기시킨다. 이것에 의한 유도방출확률 W31과 유도흡수확률 W13은 같기 때문에, 이를 Wi라 한다.
준위 3과 1의 원자수를 N3와 N1이라 하면, 단위시간 안에 준위 3에서 1로, 준위 1에서 3으로 유도천이하는 원자수는 각각 WiN3 및 WiN1이 된다. 또 준위 3으로 여기된 원자는 완화에 의해 외부에서 가해진 광과는 무관하게 준위 2 및 1로 천이한다.
이들 가운데, 천이확률 ω32로 표시되는 준위 2로 행해지는 완화가 우세하여 준위 1로 행해지는 완화는 무시할 수 있게 된다. 그러므로 완화에 의해 준위 3에서 단위시간 안에 천이하는 원자수는 ω32N3가 된다. 이상의 결과에서 준위 3의 원자수 N3가 유도천이 및 완화에 의해 변화하는 비율 dN3∕dt는
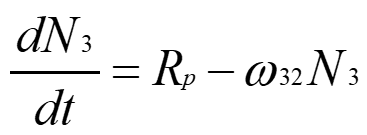
이 된다. 이 식을 비율방정식(rate equation)이라 한다. 천이확률 ω를 사용하는 대신 완화시간 τ=1∕ω을 사용하기도 한다.
준위 2로 천이한 원자는 또 완화에 의해 ω21의 확률로 바닥준위로 천이한다. 여기서 준위 2에서 1로 완화하는 것이 준위 3에서 2로 완화하는 것에 비해 대단히 늦다(ω32≫ω21)고 가정한다. 다시 말해, 준위 2의 수명이 아주 긴 경우이다. 그러면 바닥준위에서 hν의 에너지를 갖는 광에 의해 준위 3으로 여기된 원자는 매우 빠르게 천이해서 준위 2로 이동하고 그곳에 모여 있게 된다. 실제로 루비결정 안의 Cr3+이 이 경우에 해당하고, 준위 2에 모여 있는 Cr3+은 천천히 0.6943μm의 광을 방출하며 바닥준위로 되돌아간다. 결국 준위 2에 관련되는 비율방정식은 아래의 식과 같이 된다.
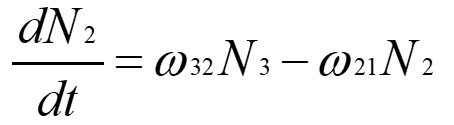
4준위 레이저는 어떨까? 우측의 그림을 보면서 따라와보자!
이 경우 준위 3에서 2로, 준위 1에서 0으로 아주 빠르게 완화하고, 준위 2에서 1로 레이저천이가 일어난다고 하자. 바닥준위와 준위 1의 에너지차 E1-E0이 열에너지 kT에 비해 대단히 클 때, 준위 1의 입자수는 무시할 수 있을 정도로 적게 된다. 이 점이 3준위계의 경우와 기본적으로 다른 것이고, 반전분포가 형성되기 쉬운 이유가 된다. 여기서 들뜬상태에서도 모든 입자가 바닥상태에 있는 것으로 하여 비율방정식을 써 보면
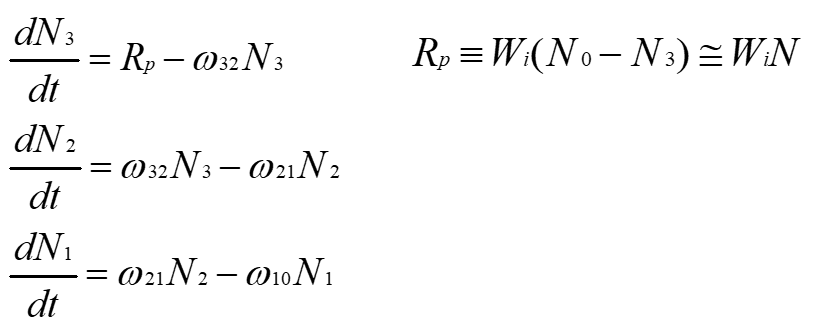
된다. 단 3준위계와 마찬가지로 상준위로 향하는 천이나 여기광 이외의 광에 의한 유도천이 등은 무시한다.
Nd:YAG레이저와 Nd:Glass레이저 등이 4준위 레이저의 대표적인 예이다.
'Optics > Laser optics' 카테고리의 다른 글
| 7. 레이저 발진조건 (1) | 2023.12.27 |
|---|---|
| 6. 레이저의 이득계수와 증폭 (0) | 2023.12.26 |
| 4. 레이저의 반전분포 (0) | 2023.12.24 |
| 3. 광의 흡수와 방사 그리고 유도방출 (1) | 2023.12.23 |
| 2. 원자의 에너지 준위, 여기와 들뜬상태 (1) | 2023.12.22 |



