


레이저발진
반전분포상태인 원자계의 매질 안에서는 천이의 스펙트럼 폭에 해당하는 주파수의 전자파가 증폭된다는 것을 알았다. 다음으로 이 같은 레이저매질이 광공진기 안에 있을 경우를 생각해 보자. 전자파가 두 개의 반사거울 사이를 왕복하면서 레이저매질을 통과하기 때문에 증폭작용이 일어난다.
증폭이 반사거울의 불완전한 반사나 레이저매질 안에서 산란으로 생기는 손실을 상회할 경우, 공진기 안에 축적되는 방사에너지는 시간이 경과하면서 증가되어 간다. 이 때문에 이득의 포화효과로 증폭률이 감소하고, 발진준위가 높아지며, 결국 포화된 이득이 손실과 같아지는 점에 이르게 된다. 이 점에서는 이득에서 손실을 공제한 실질적인 이득인자는 1이 되고, 전자파의 강도는 증가하지 않게 된다. 다시 말해, 정상 발진상태가 되는 것이다.
발진 조건

두 장의 거울로 페브리-페로 공진기를 구성하고, 레이저매질을 공진기 안에 삽입하면 레이저 발진기가 된다. 적당한 여기에 의해 반전분포상태가 되고, 이것에 의한 증폭작용이 거울의 반사손실, 회절손실 및 매질 안에서의 손실 등을 상회하면 레이저는 발진하게 되는 것이다.
위 그림은 발진기의 가장 간단한 예로서 페브리-페로 공진기 안에 레이저매질이 가득 찬 상태를 나타내고 있다. 레이저가 발진되기 위해서는 공진기 안의 레이저광이 발진조건을 만족시킬 때까지 여기에너지를 흡수하며 공진기 안에서 왕복운동을 하기 때문에 레이저 발진기의 전출력강도는, 전파정수 Γ(ν)를 이용하여 표현하면,
(레이저 발진기의 출력 강도는 아래의 식으로 주어진다.)
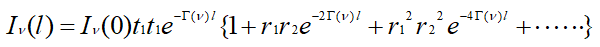
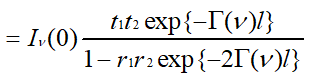
로 주어진다. l은 공진기 길이로 매질의 길이와 같다고 가정하고, r1과 r2는 공진기를 구성하는 두 거울의 진폭 반사계수를 말한다. t1과 t2는 공진기에서 두 거울의 진폭 투과계수이다.
그리고 분모가 0이 되는 r1r2exp{-2Γ(ν)ㅣ}=1이면, 입사광이 0이어도 출력광은 유한하며, 공진기 안의 한 점에서 출발한 광이 1회 왕복한 후에도 진폭은 동일하고 위상은 2π의 정수배 만큼 차이가 생겨 위상도 동일하기 때문에 발진조건을 진폭과 위상으로 나누어 표현할 수 있다. 여기서 이득계수와 관련되는
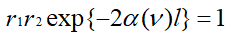
은 진폭조건으로
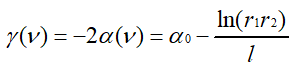
가 되며, 위상조건은
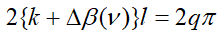
가 된다. 여기서 q는 양의 정수이고, 진폭조건에서는 공진기 안에 분포하는 수동성 손실을 고려한 감쇠항 αo를 더한 것이다. 한편 r1과 r2는 1보다 작기 때문에 -ln(r1r2)는 양수가 된다.
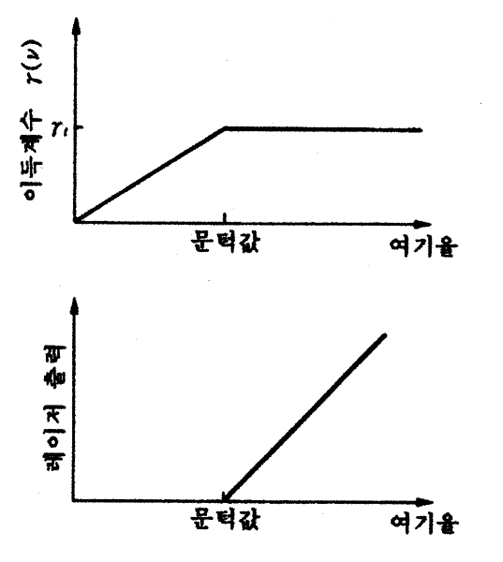
레이저매질은 여기시키지 않은 상태에서는 반전분포를 얻을 수 없고, γ(ν)는 음수가 되어 흡수작용을 하게 된다. 여기를 강하게 하면 먼저 반전분포가 되어 증폭작용을 한다. 그러나 증폭도가 낮을 때는 거울이나 매질의 손실 때문에 발진은 일어나지 않는다. 여기량을 늘려 반전분포량이 충분히 커지면 이득계수 γ(ν)가 증가하고 이것이 손실을 극복했을 때 레이저는 발진하기 시작한다.
α0는 공진기 안의 수동성 손실을 고려한 감쇠항이고, k=ω(μ0ε)1/2은 유도천이가 없을 때의 위상정수이며, Δβ(ν)는 유도천이에 의한 위상변화이다. 이들과 이득계수를 이용하면 발진문턱 조건은
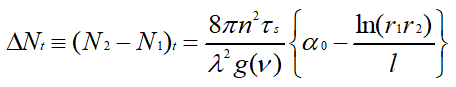
가 된다. 발진문턱값에 도달한 후 여기량을 더욱 증가시키면 언뜻 보기에 γ(ν)는 γt(ν)보다 커지는 것으로 생각할 수도 있다.
[참고] 발진조건
그러나 실제로 정상적 발진상태에서는 여기를 강하게 하여도 γ(ν)=γt(ν) 이상은 되지 않는다.
매질의 포화현상에서 일단 레이저가 발진하기 시작하면, 발진광이 유도방출 및 흡수하는 입자수에 영향을 주어 반전분포량 즉, 이득계수가 포화되어 γ(ν)는 γt(ν) 보다 커지지 않는다.
역으로 생각하면 포화 이득계수가 γt(ν)와 같게 되는 강도에서 정상 발진하는 것이 된다. 유도천이확률 Wi는 공진기 안의 레이저 강도 Iν에 비례하고, 레이저 발진기의 출력은 Iν에 거울의 투과계수를 곱한 것이 되어 여기를 강하게 하면, 발진 시작 이후의 출력은 직선적으로 증가하게 된다.
'Optics > Laser optics' 카테고리의 다른 글
| 9. 레이저 제어기술, Q-스위치 (0) | 2023.12.29 |
|---|---|
| 8. 레이저의 발진모드, 종모드와 횡모드 (1) | 2023.12.28 |
| 6. 레이저의 이득계수와 증폭 (0) | 2023.12.26 |
| 5. 3준위 및 4준위 레이저 비율방정식 (0) | 2023.12.25 |
| 4. 레이저의 반전분포 (0) | 2023.12.24 |



