


앞에서 설명했던 것처럼 자연방출 및 유도방출에 의해 준위 2에서 1로 천이하는 확률은 관계가 있음을 알 수 있다.
실제로는 전자파의 강도 Iν가 아주 클 경우에는 자연방출의 효과는 무시한다.
실제로 레이저매질은 1cm3당 고체의 경우 10^18~10^20개, 기체의 경우에도 10^10~10^15개 정도의 원자(이온 혹은 분자)를 갖고 있다. 이들은 각기 다른 에너지준위에서 운동하고 있다.
이들에 주파수 ν의 전자파를 가하면, 흡수에 의해 단위시간 및 단위체적당 W12(ν)N1개의 원자가 준위 1에서 2로 천이하여 hνW12(ν)N1에 해당하는 광파워를 원자계에 준다. 동시에 유도방출에 의해 단위시간 및 단위체적당 W21(ν)N2개의 원자가 준위 2에서 1로 천이하며, hνW21(ν)N2에 해당하는 광파워를 원자계에서 전자파로 주게 된다.
반전분포
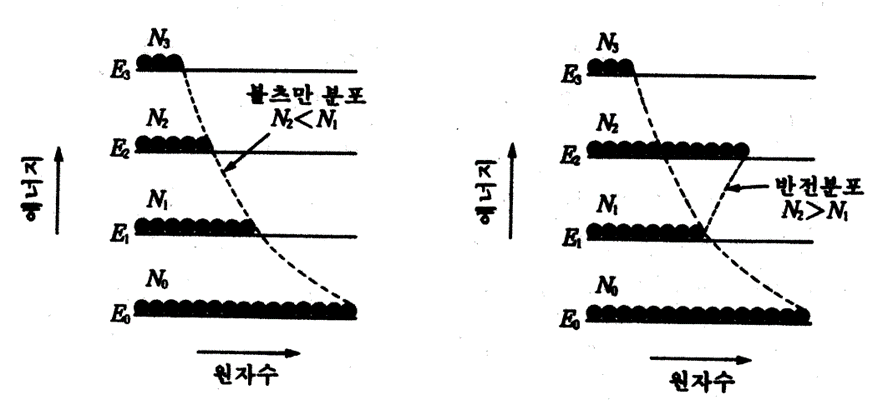
열평형상태에서 원자수는 볼츠만 분포로 표현되는 에너지분포를 나타낸다.
볼츠만 분포에서 E1의 원자수를 N1, E2의 원자수를 N2라 할 때,
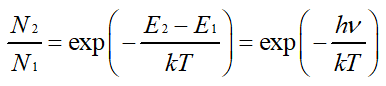
T는 절대온도이며 k=1.38×10-23J∕K는 볼츠만 상수이다.
E2>E1에서 N2<N1상태의 분포를 형성한다. 이 경우에는 여기에너지를 더욱 증가시켜도 이 분포가 변화하지 않기 때문에 광은 증폭되지 않는다.
원자는 종류에 따라서 원자 특유의 에너지준위 안에 수명이 긴 에너지준위인 준안정상태의 준위를 갖는 것이 있다. 그림의 에너지준위 E2와 E1에서 원자의 수명을 각각 τ2와 τ1이라 할 때
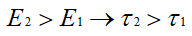
이 된다. 다시 말해, E1보다 E2가 원자 존재조건이 좋아 평균수명이 길고, 역으로 E1의 존재조건이 좋지 않아 수명이 짧은, 다른 두 에너지준위를 갖는 원자가 생긴다. 이 같은 원자를 점차 여기시키면
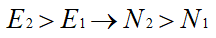
이 되는데 이 같은 상태를 반전분포(population inversion)라 한다.
이런 반전분포상태는 볼츠만 분포 조건을 만족시키기 위해서 절대온도 T가 0도 이하인 부온도(negative temperature)상태를 만들어야 한다는 것이 된다. 그러나 절대온도에서 0도 이하는 실제 존재하지 않는 것이지만, 이 같은 반전분포의 상태를 부온도분포라고도 한다. 이렇게 반전분포상태를 만드는 것은 광의 유도방출에서 필수조건이고, 반전분포를 연속적으로 만드는 것이 광을 연속적으로 증폭시키는 조건이 된다.
'Optics > Laser optics' 카테고리의 다른 글
| 6. 레이저의 이득계수와 증폭 (0) | 2023.12.26 |
|---|---|
| 5. 3준위 및 4준위 레이저 비율방정식 (0) | 2023.12.25 |
| 3. 광의 흡수와 방사 그리고 유도방출 (1) | 2023.12.23 |
| 2. 원자의 에너지 준위, 여기와 들뜬상태 (1) | 2023.12.22 |
| 1. 레이저와 결맞음은 뭘까? (0) | 2023.12.21 |



