


Bohr의 양자 조건
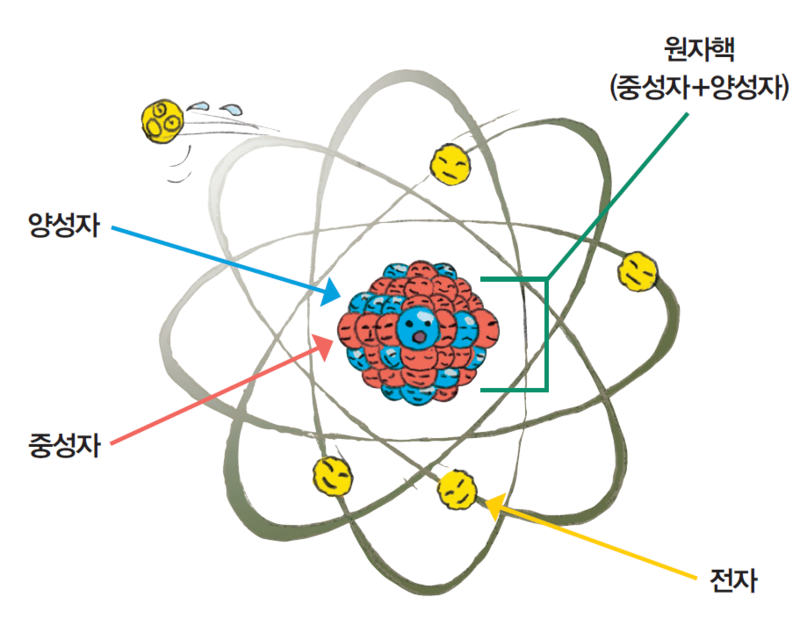
모든 물질은 원자로 구성되며, 각 원자는 보아의 원자모형으로 잘 알려진 것같이 원자핵과 그 주위를 원운동하고 있는 음전하의 전자군으로 구성되어 각자 에너지를 갖고 있다. 원자가 갖는 전자수는 원자의 종류에 따라 다르다. 원자핵 주위를 원궤도로 도는 전자는 그림 2-1에 나타낸 것같이 일정한 반지름을 갖는 특정한 궤도만이 허용된다. 즉 그 전자가 갖는 운동량(질량×속도) p와 궤도길이의 곱은 임의의 수의 정수 배 값만 취할 수 있다는 것이 된다. 이를 식으로 나타내 보자. 전자의 질량을 m, 속도를 , 그리고 궤도의 길이를 2πr이라 하면
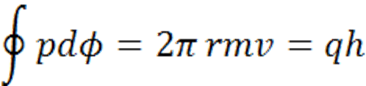
의 관계가 성립하고, 이 식은 보아의 양자조건(quantum condition)을 잘 설명하고 있다. 여기서 q는 양의 정수로 양자수(quantum number)라 하고, h=6.626×10-34J‧s는 플랑크 상수이다. 이것은 전자가 취할 수 있는 궤도는 제한되어 있고, 전자는 일정한 간격을 유지하는 궤도에서만 안정하다는 것이 된다. 이와 같이 양자조건에 의해서 주어지는 에너지 값을 에너지준위라 한다.
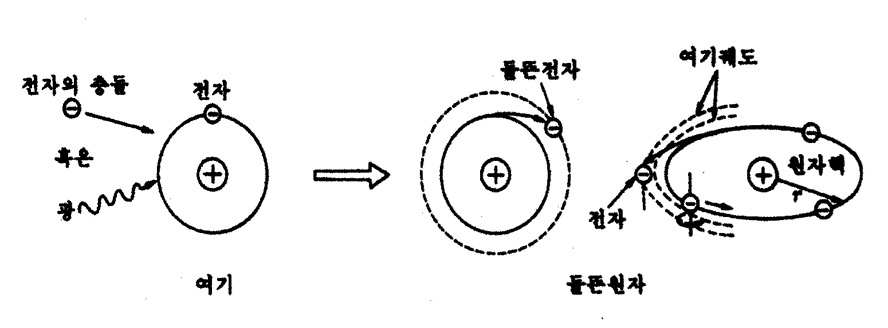
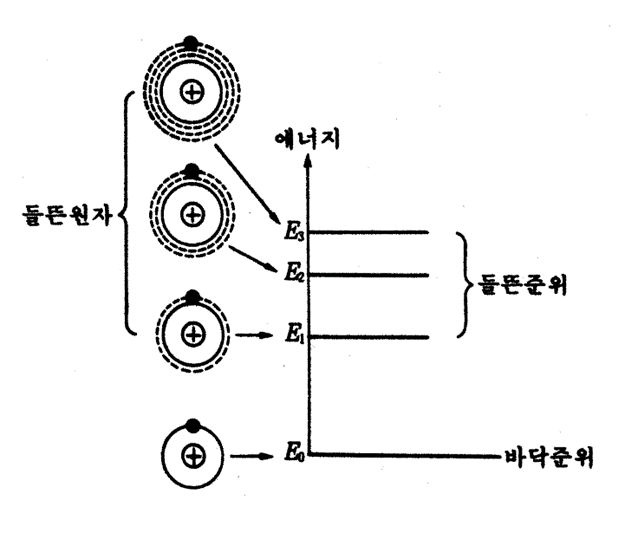
원자의 첫 번째 최외각 궤도를 도는 전자에 외부에서 다른 전자를 충돌시키는 등 에너지를 부여하면, 전자는 보다 바깥쪽의 궤도로 이동하게 된다. 즉 전자는 원래의 상태보다 큰 에너지를 갖게 되고, 다른 운동을 하게 되는 것이다. 이러한 상태를 전자가 에너지를 얻어 들뜬상태(excited state)에 있다고 하고, 이와 같이 전자나 원자에 에너지를 주는 것을 여기(pumping)라 한다. 또 여기 이전의 에너지가 가장 낮은 q=1에 대응하는 전자의 상태를 바닥상태(ground state)라 한다.
원자핵 주위를 원궤도로 도는 전자는 일정한 반지름을 갖는 특정한 궤도만이 허용되고, 전자는 일정한 간격을 유지하는 궤도에서만 안정하다. 양자 조건에 의해서 주어지는 에너지값을 에너지준위라 한다.
Bohr의 진동수 조건
\[ \left| E_i - E_f \right| = \Delta E = h \nu \]
원자의 천이주파수는 두 에너지준위의 차에 의해서 결정된다.
두 준위의 에너지차에 해당하는 광자를 방출 혹은 흡수.
'Optics > Laser optics' 카테고리의 다른 글
| 6. 레이저의 이득계수와 증폭 (0) | 2023.12.26 |
|---|---|
| 5. 3준위 및 4준위 레이저 비율방정식 (0) | 2023.12.25 |
| 4. 레이저의 반전분포 (0) | 2023.12.24 |
| 3. 광의 흡수와 방사 그리고 유도방출 (1) | 2023.12.23 |
| 1. 레이저와 결맞음은 뭘까? (0) | 2023.12.21 |



