


레이저 증폭에서 이득(gain)과 반전분포량의 관계에 대해서 생각해 보자. 광의 진행방향을 레이저매질의 길이 l방향으로 하고 단위면적당 광강도를 Iν, 이득계수를 γ(ν)라 하면, 광의 강도변화량은 아래의 식 관계로 표현할 수 있고, 그 해는 또한 다음과 같다.
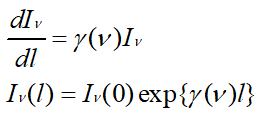
이 된다. 레이저 작용이 준위 2와 1 사이의 유도천이에 의해서 일어난다고 할 때 원자계에서 전자파에 주어지는 단위체적당 광파워는
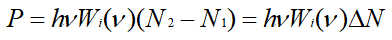
이 되고, 이것은 Iν의 증가량 dIν/dl과 같기 때문에 유도천이의 비를 이용하면 이득계수는 다음과 같이 표현된다.

광이 길이 l의 증폭성 매질을 일정한 이득계수로 통과한 후의 증폭도를 G라 하면


이 된다. 광의 증폭도는 이론적으로 반전분포 원자수가 많을수록, 광이 통과하는 증폭매질의 길이가 길수록 지수함수적으로 증가한다.
한편, 전 포스팅에서는 비율방정식에서 반전분포량을 구하는 데 레이저천이가 일어나는 준위 사이의 유도천이(Wi=W21) 영향은 무시했다. 반전분포만을 얻기 위한 조건을 구하는 데는 이것으로도 좋으나, 레이저가 발진 혹은 증폭하는 경우에는 강한 레이저광에 의한 유도천이를 무시할 수 없게 된다. 이상화된 4준위 레이저의 경우, 유도천이의 항 Wi(N1-N2)를 가감해 주어야 한다. 이것으로 반전분포량을 구하면
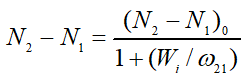
이 된다. 여기서 (N2-N1)o는 Wi=0에 대한 N2-N1의 값으로 식 (2-41)을 의미한다. Wi는 여기광의 강도가 아닌 레이저광의 강도 Iν에 비례한다. 그러므로 일정한 여기율 Rp의 조건에서라도 Iν 값이 커지면 반전분포량이 감소한다는 것을 알 수 있다. 이것을 포화현상(saturation)이라 한다. 이득계수 γ(ν)에서도 같은 포화현상이 일어나게 마련이다.
'Optics > Laser optics' 카테고리의 다른 글
| 8. 레이저의 발진모드, 종모드와 횡모드 (1) | 2023.12.28 |
|---|---|
| 7. 레이저 발진조건 (1) | 2023.12.27 |
| 5. 3준위 및 4준위 레이저 비율방정식 (0) | 2023.12.25 |
| 4. 레이저의 반전분포 (0) | 2023.12.24 |
| 3. 광의 흡수와 방사 그리고 유도방출 (1) | 2023.12.23 |



