


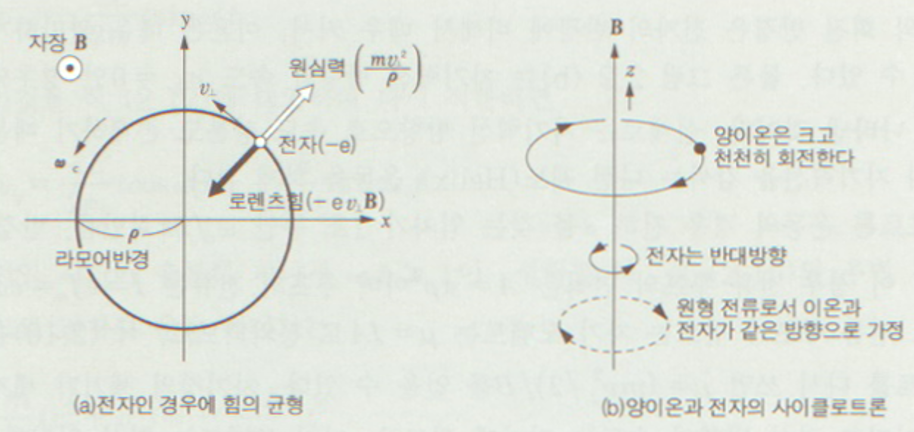
자기장이 인가되었을 때 진행하는 입자의 속도 벡터는 자기장에 의해 작용하는 힘에 의해 자기력을 받음.
자장 안에서 하전 입자의 운동 방정식:
\( m \frac{d\vec{v}}{dt} = q\vec{v} \times \vec{B} = I \times \vec{B} \) ; 로런츠의 원 운동식
입자가 속도 \( V \)를 지니고 있을 때 그에 대한 전자의 로런츠 힘(자기장력)이 작용하기 때문에 원운동을 함.
사이클로트론 운동, 라모어 운동
운동량 \( \frac{mv^2}{\rho} \) = 전기력 \( -eV_1\vec{B} \), \( v_1 \): 입자의 속도
회전 주파수(사이클로트론 주파수): \( f_c = \frac{\omega_c}{2\pi} = \frac{eB}{2\pi m} \)
회전 반경(라모어 반경): \( \rho = \frac{v_1}{\omega_c} = \frac{mv_1}{eB} \)
시간에 따라 변하지 않는 경우: 편향하며 이동
\( v_D = \frac{q\vec{E}}{m\nu} \)
전장이 시간에 따라 변하는 경우(조화 진동): \( E(t) = E_0 \cos \omega t \)
충돌이 없는 경우 (\( \nu=0 \)):
\( v(t) = \frac{qE_0}{m} \sin \omega t \) ; 전장과 입자의 속도는 위상차가 90도 나기 때문에 시간에 대한 평균값이며, 가속과 감속이 서로 상쇄되어 한 주기 전장에 의한 평균 속도는 0임.
입자가 충돌이 존재: 전자와 이온의 충돌빈도가 90도 회전함.
\( v(t) = \frac{q E_0}{m \sqrt{\nu^2 + \omega^2}} \sin(\omega t + \theta) \) \( \theta = \tan^{-1}\left(\frac{\omega}{\nu}\right) \)
충돌에 의해 입자의 운동과 전장의 위상이 어긋남.
이로 한 개의 한 주기 시간 \( T=2\pi/\omega \) 동안 충돌하는 방법:
\( P_a = \frac{1}{T} \int_{0}^{T} qv(t)E(t)dt = \frac{1}{2} q^2 \frac{\nu}{m \nu^2 + \omega^2} E_0^2 \) 이 된다.
'Semiconductor > Plasma' 카테고리의 다른 글
| 21. Plasma 충돌 현상 (0) | 2023.12.18 |
|---|---|
| 20. 전자 사이클로트론 공명 (1) | 2023.12.18 |
| 18. 하전입자의 운동 (전기장) (1) | 2023.12.17 |
| 17. 플라즈마의 기초방정식 (0) | 2023.12.16 |
| 16. 플라즈마의 기준 (1) | 2023.12.15 |



