21. Plasma 충돌 현상

 

n플라즈마 내부에서는 전자(e), 이온(i) 및 중성입자(n)의 3종류 입자들이 서로 충돌하면서 진행

n쿨롱 충돌(하전입자 간의 충돌→쿨롱 힘이 작용) :  ① e-i, ② e-e, ③ i-I

n역학적 충돌(적어도 하나의 중성입자가 충돌 대상→접촉 순간에만 힘이 작용) :  ④ e-n, ⑤ i-n, ⑥ n-n

 

 

n 단단한 구에 충돌돌하는 단면적적: 거의 입자 크기에 의해 결정

 

 

n  이온과 중성입자  (③ i-i, ⑤ i-n, ⑥ n-n) :

n 전자와 입자 (① e-i, ④ e-n) :

 

 

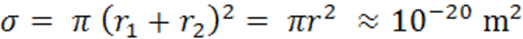
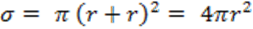
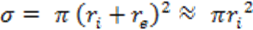
평균 자유 행로(Mean Free Path) : 충돌에서 다음 충돌까지 이동하는 거리

\( \lambda_{12} = \frac{1}{n_2 \sigma} \) : 입자 2가 산포하고 있다고 가정, 입자 1이 2에 충돌

 

\( \lambda_{nn} = \lambda_{en} /\sqrt{4/2} \) : n-n 충돌은 서로 같은 속도로 움직이기 때문에 상대속도는 더욱 커지고 충돌 횟수가 증가하게 되어 평균 자유행정거리는 짧아진다.

 

\( \lambda_{nn} > \lambda_{in} \) ; 이온은 중성입자보다 운동량이 높다.

 

충돌 주파수(Collision Frequency) : 단위 시간당 평균 충돌 횟수

 

\( f_{12} = \frac{\langle v_1 \rangle}{\lambda_{12}} \) ; \( \langle v_1 \rangle \)는 입자 1의 평균 속도

 

쿨롱 충돌 :

• 쿨롱힘 가운데 충돌을 모형화함(\( \propto 1/r^2 \)) 자유로 충돌때까지 무한대의 거리면서 작용
• 그룹조직 안에서의 충돌은 충돌회피(Multi-Body Collision)
  • 충돌조직은 아주 많은 하전입자로 구성
• Debye Field 범위 안에서 상호충돌(순 빌보다 90° 휘어진 충돌을 일으키는 경우
  • 이온에 의한 충돌이 실질적으로 작용하는 대표이 길이 안에서 제한적으로 작용
• 대비하여, 플라즈마 밖에서는 빠른 빌레이를 하는 하전입자들의 단단한 방상

탄성충돌에 의한 에너지 전달

• 탄성충돌 : 충돌 전에 있는 입자의 영격각이 보존존되는 경우
• 충돌 1이 전해 있는 입자(속도 \( v_2=0 \))와 충돌하면, 운동량 및 입자의 보존 이론으로부터

\( v' = \frac{2m_1}{m_1 + m_2} v_1 \)

 

정면 충돌일 때 입자 1의 에너지 손실(Energy Loss Factor) :

\( k = - \frac{\Delta \epsilon}{\epsilon_1} = - \frac{(1/2)m_2 v^2}{(1/2)m_1 v_1^2} = \frac{4m_1 m_2}{(m_1 + m_2)^2} \)

두 입자가 충돌에 대해 각도로 비스듬히 충돌하는 경우 :

• 손실에너지가 위의 결과의 50%에 해당 <- cosθ로 표시고 모든 모델에 대해 평균화한다.
• n-n, i-n 충돌은 \( k \approx 0.5 \) <- 무거운 입자 간의 충돌(예: \( m_1 \approx m_2 \))
• e-n, e-i 충돌은 \( k \approx (2m_e/m_n) \times 10^{-4} <- 전자로 부터의 거친 에너지는 거의 없다.

→ 전자의 에너지 손실계가 아주 크다. 우리는 플라즈마 : \( T_e > T_i > T_n \) (순서, 순서에 의한 상태) : \( T_e \approx T_i \approx T_n \)