


전자 사이클로트론 공명
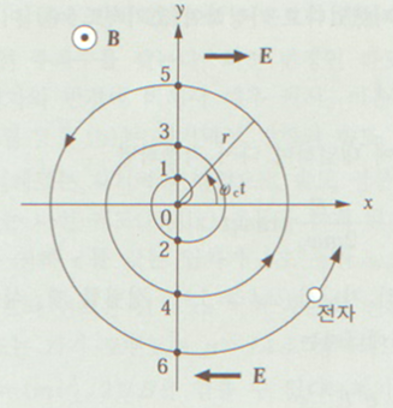
자기장 안에 사이클로트론 운동을 하고 있는 전자에 외부에서 주파수가 \( \omega \)의 고주파 전압을 인가하면 전자는 \( \omega = \omega_c \)일 때 전자가 공명되어 회전 속도로 에너지를 받아 가속되는 현상 → Electron Cyclotron Resonance ; ECR
(예를 들어, 방향으로 전자 \( E \sin \omega t \)가 인가되었을 때, 자장 안에서 전자의 방정식을)
\( \frac{dv_x}{dt} = -e v_y B - e E \sin \omega t \)
\( \frac{dv_y}{dt} = e v_x B \)
→
\( \frac{d^2 v_x}{dt^2} + \omega_c^2 v_x = - \frac{e E \omega_c}{m} \cos \omega t \)
(t=0에서 전자가 정지했다고 가정하고, 이 방정식의 해를 구하면)
\( v_x = - \frac{e E}{2m} t \sin \omega t \)
\( v_y = \frac{e E}{2m} t \cos \omega t - \frac{e E}{2m \omega_c} \sin \omega t \)
(시간이 충분히 지난 후 \( \omega t \gg 1 \) 상황할 때, 우리는 각속도가 무시 가능하므로 전자의 운동에너지; 전자는 나선형 행보로 가속됩니다.)
\( \frac{m}{2} (v_x^2 + v_y^2) = - \frac{e^2 E^2}{8m} t^2 \)
Lorentz Force:
\( \frac{d\vec{v}}{dt} = q (\vec{E} + \vec{v} \times \vec{B}) \)
(하지만 이 방정식을 하면 다른 모든 운동을 한다.)
(속도 \( \vec{v} \)는 회전운동 중심속도 \( \vec{u} \)와 속도의 중심속도에서 사이클로트론 운동의 속도 \( \vec{u}_D \)와의 합으로 가장)
\( \vec{v} = \vec{u} + \vec{E} \times \vec{B} / B^2 \)
(• Cyclotron 운동 \( \omega \):)
\( \frac{d\vec{\omega}}{dt} = q \vec{u} \times \vec{B} \)
(• 평균운동 중심속도 \( \vec{u}_D \)는:)
\( \vec{u}_D = \vec{E} \times \vec{B} / B^2 \) → \( \vec{u}_D \approx E/B \)
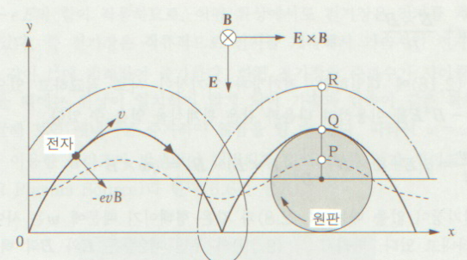
전•자장에서 하전입자의 운동
\( \frac{d^2\vec{v}}{dt^2} = q (\vec{E} + \vec{v} \times \vec{B}) \)
(하지만 이 방정식을 하면 다른 모든 운동을 한다.)
(속도 \( \vec{v} \)는 회전운동 중심속도 \( \vec{u} \)와 속도의 중심속도에서 사이클로트론 운동의 속도 \( \vec{u}_D \)와의 합으로 가장)
\( \vec{v} = \vec{u} + \vec{E} \times \vec{B} / B^2 \)
(Cyclotron 운동 \( \omega \):)
\( \frac{d\vec{\omega}}{dt} = q \vec{u} \times \vec{B} \)
(평균운동 중심속도 \( \vec{u}_D \)는:)
\( \vec{u}_D = \vec{E} \times \vec{B} / B^2 \) → \( \vec{u}_D \approx E/B \)
'Semiconductor > Plasma' 카테고리의 다른 글
| 22. 원자의 여기와 이온 (0) | 2023.12.19 |
|---|---|
| 21. Plasma 충돌 현상 (0) | 2023.12.18 |
| 19. 하전입자의 운동 (자기장) (1) | 2023.12.17 |
| 18. 하전입자의 운동 (전기장) (1) | 2023.12.17 |
| 17. 플라즈마의 기초방정식 (0) | 2023.12.16 |



