


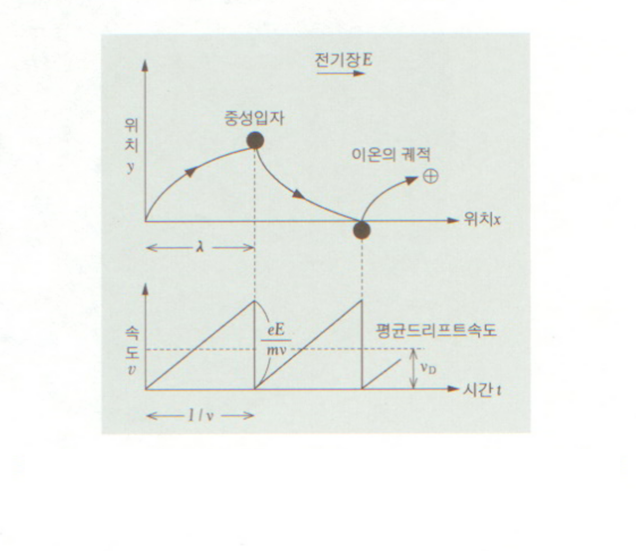
직류(DC) 방전에서 전자에 관련된 경우 Drift 운동 : 플라즈마 안에서 흐르는 평균자유행로의 길이에 의해, 이온은 전자보다 훨씬 큰 자유행로를 가짐(예시, 토머스) 또는 충돌하여 전자가 손실되어 이동할 수 있는 것
\( \frac{d\vec{v}}{dt} = \frac{q\vec{E}}{m}; \) Newton 운동방정식
\( \frac{d\vec{v}}{dt} = \frac{q\vec{E}}{m} - \nu\vec{v}; \) Langevin 방정식(이온이 대기 중에 마찰력을 겪음)
\( \nu \): 충돌주파수 (이온이 중성 입자와 대기 사이에 충돌을 하게 됨)
\( v_D = \frac{qE}{m\nu}; \) Drift속도(평균자유행로의 수학 이동속도)
시간에 따라 변하지 않는 경우 : 편이하며 이동한다. \( v_D = \frac{qE}{m\nu} \)
전장이 시간에 따라 변하는 경우(조화진동) : \( E(t) = E_0 \cos \omega t \)
충돌이 없는 경우(\( \nu = 0 \)) \( v(t) = \frac{qE_0}{m} \sin \omega t; \) 전장과 입자의 속도는 위상차가 90도 나기 때문에 시간에 대한 평균값이다, 가속과 감속이 서로 상쇄되어 1주기 전장에 의한 평균 속도는 0이 된다.
입자가 충돌이 존재 : 전자와 이온의 충돌빈도가 90도 회전한다.
\( v(t) = \frac{qE_0}{m \sqrt{\nu^2 + \omega^2}} \sin(\omega t + \theta) \); 충돌에 의해 입자의 운동과 전장의 위상이 어긋난다.
\( \theta = \tan^{-1}\left(\frac{\omega}{\nu}\right) \)
이로 1개의 1주기 시간 \( T = \frac{2\pi}{\omega} \) 동안 충돌하는 방법
\( P_a = \frac{1}{T} \int_0^T qv(t)E(t)dt = \frac{q^2 E_0^2}{2m (\nu^2 + \omega^2)} \nu \)
'Semiconductor > Plasma' 카테고리의 다른 글
| 20. 전자 사이클로트론 공명 (1) | 2023.12.18 |
|---|---|
| 19. 하전입자의 운동 (자기장) (1) | 2023.12.17 |
| 17. 플라즈마의 기초방정식 (0) | 2023.12.16 |
| 16. 플라즈마의 기준 (1) | 2023.12.15 |
| 15. Plasma 식각의 종류 (0) | 2023.12.15 |



