


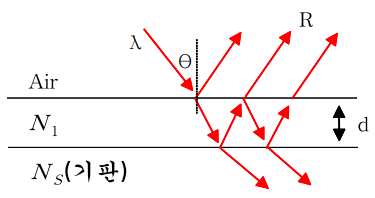
위 그림처럼 굴절률인 투명기판에 굴절률이고, 기하광학적 두께가 d인 균질한 투명막을 한층 쌓은 경우를 생각해보자.
파장λ인 빛이 수직으로 입사하여 ψ=0°가 될 때의 반사율 R은 다음과 같이 구해진다.
\[ R = 1 - \frac{4 N_{2} N_{1}^{2} N_{S}}{N_{1}^{2} (N_{2} + N_{S})^{2} - (N_{1}^{2} - N_{S}^{2}) \sin^{2} \left( \frac{\sigma}{2} \right)} \] \[ \sigma = \frac{4\pi}{\lambda} N_{1}d \]
여기서 반사율이 극값을 이룬 조건을 파장 λ = λ0일 때에 대하여 조사해보면 광학적 두께 \( N_1d \)가
\[ N_1d = \frac{\lambda_0}{4} (2m+1) \quad \text{또는} \quad N_1d = \frac{\lambda_0}{4} 2m \quad (m = 0, 1, 2, \ldots) \]
일 때 극대값 또는 극소값을 이루는 것을 알 수 있다. 이때
\[ N_1d = \frac{\lambda_0}{4} (2m+1) \quad \text{인 경우는 막의 반사율은} \quad N_1 \quad \text{이} \quad N_s \quad \text{보다 크거나 또는 작음에 따라서 극대값 또는 극소값을 이루고,} \]
\[ N_1d = \frac{\lambda_0}{4} (2m) \quad \text{인 경우에 막은 막의 특성 행렬이 파장} \quad \lambda_0 \quad \text{에서는 단위 행렬로 된다. 따라서 파장} \quad \lambda_0 \quad \text{에서 막이 존재하지 않는 기판의 반사율과 같게 된다. 따라서 무반사 박막이 될 조건은} \]
\[ N_1d = \frac{\lambda_0}{4} (2m+1) \quad \text{에서 막의 굴절률이 기판의 굴절률보다 작은 (} N_1 < N_s \text{) 것이 필요하다.} \]
\[ N_1d = \frac{\lambda_0}{4} (2m+1) \quad \text{일 때의 반사율을 구하면} \]
\[ R = \left( \frac{N_1 N_s - N_1^2}{N_1 N_s + N_1^2} \right)^2 \]
가 된다.
\( R=0 \)이 될 조건은 \( N_1 = \sqrt{N_2 N_s} \) 이다.
따라서 단층 무반사 박막에서는 \[ N_1d = \frac{\lambda_0}{4} (2m+1) \quad (m= 0, 1, 2, \ldots) \] 의 2개의 조건이 필요하다.
위상조건(막두께에 관계한 식)으로 하여, 단층 무반사 박막에서는 통상 \( m=0 \)을 이용한다.
진폭조건(굴절률에 관계한 식)으로 하여 통상 입사매질은 공기이면 \( N_2=1 \)이다.
예를 들면 기판으로 \( N_s=1.52 \)의 유리를 사용하면 \[ N_1 \approx \sqrt{1.52} \approx 1.23 \]
이처럼 막을 \( N_1d = \frac{\lambda_0}{4} \) 가 되도록 코팅하면 파장 \( \lambda_0 \)에서 반사율은 완전히 0이 된다.
그러나 실제로는 이러한 낮은 굴절률을 갖는 증착물질이 없기 때문에 현재에는 가능한 한 굴절률이 작고 물리, 화학적으로 안정되고 내구성이 좋은 증착물질로서 \( MgF_2 \) ( \( N_1 \approx 1.38 \) ) 이 사용되고 있다.
\( MgF_2 \)를 \( N_s=1.52 \) 인 유리에 \( N_1d = \frac{\lambda_0}{4} \) 가 되도록 코팅하면, 파장 \( \lambda_0 \)에서의 반사율은 약 1.26%가 되고, 기판의 반사율 4.26%와 비교하면 반사율은 꽤 감소함을 알 수 있다.
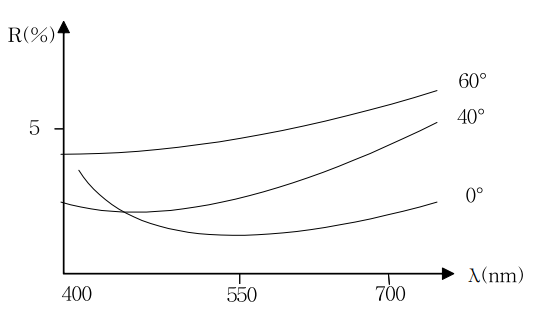
그러나 수직입사하지 않는 경우는 극소값의 반사율은 크게 되어 단 파장측으로의 이동되게 됨을 주의할 필요가 있다.
'Optics > Wave optics' 카테고리의 다른 글
| 5. 박막 두께 측정은 어떻게 하는가? (0) | 2023.11.30 |
|---|---|
| 4. 진공에 대해 자세히 알아보자 (1) | 2023.11.29 |
| 3. 다층 무반사 박막 설계를 해보자. (1) | 2023.11.28 |
| 1. 진공 증착에 대하여 (0) | 2023.11.28 |



