


다층 무반사 박막
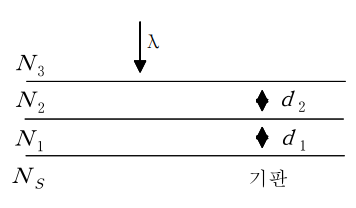
다층 무반사 박막의 구성은 다층막의 특성 행렬을 계산하여, \( R=0 \)이 되는 위상 및 진폭조건을 해석하여 얻어진다. 단층무반사 박막과 같은 모양으로 굴절률 \( N_s \)인 투명기판에 굴절률 \( N_1, N_2 \)이고 기하학적 두께가 \( d_1, d_2 \)인 균질한 투명막이 다층으로 쌓인 경우를 생각해보자. 입사매질은 앞에서 기술한 것처럼 보통은 공기이면서 \( N_3=1 \)로서 파장 \( \lambda \)의 빛이 수직으로 입사한다. 각층의 특성행렬은 아래와 같다. 다층막의 합성특성행렬은 각층의 특성행렬의 곱으로 된다.
\[ \begin{pmatrix} \cos \beta_2 & -i N_2 \sin \beta_2 \\ -i \frac{\sin \beta_2}{N_2} & \cos \beta_2 \end{pmatrix} \begin{pmatrix} \cos \beta_1 & -i N_1 \sin \beta_1 \\ -i \frac{\sin \beta_1}{N_1} & \cos \beta_1 \end{pmatrix} = \begin{pmatrix} m_{11}' & m_{12}' \\ m_{21}' & m_{22}' \end{pmatrix} \]
여기서 \( \beta_1 = \frac{2\pi}{\lambda}N_1 d_1 \), \( \beta_2 = \frac{2\pi}{\lambda}N_2 d_2 \)이다. 행렬식을 풀면
\[ \begin{aligned} m_{11} &= \cos \beta_1 \cos \beta_2 - N_1 N_2 \sin \beta_1 \sin \beta_2 \\ m_{12} &= -i \left( \frac{\sin \beta_1 \cos \beta_2}{N_1} + \frac{\cos \beta_1 \sin \beta_2}{N_2} \right) \\ m_{21} &= -i \left( N_1 \sin \beta_1 \cos \beta_2 + N_2 \cos \beta_1 \sin \beta_2 \right) \\ m_{22} &= \cos \beta_1 \cos \beta_2 - \frac{N_2 N_1 \sin \beta_1 \sin \beta_2}{N_2 N_1} \end{aligned} \]
반사율은 위의 주어진 식으로부터 반사율이 0이 되는 조건은 식의 분자가 0이 될 때이다.
투명막의 경우 \( m_{11}, m_{22} \)은 실수이며, \( m_{12}, m_{21} \)은 순허수이어서
실수부 : \( m_{11} P_1 - m_{22} P_l = 0 \)
허수부 : \( m_{12} P_1 + P_l m_{21} = 0 \)
\( P_1 = 1 \), \( P_l = N_s \) 가 다층 무반사 박막의 조건이 된다. 풀이는 여러 가지 있으니 참고만 하시라...
(A) V coating \( (N_1d_1 = N_2d_2 = \frac{\lambda_0}{4}) \)
이 무반사 박막은 파장 \( \lambda = \lambda_0 \)에서 반사율이 극소값을 보이고 분광반사율곡선이 V와 비슷하다는 데에서 V-coat로 불리어진다.
위상조건이 \( N_1d_1 = N_2d_2 = \frac{\lambda_0}{4} \)일 때, 기준파장 \( \lambda_0 \)에서의 진폭반사율을 구하여 보자. \( \lambda = \lambda_0 \)이므로 \( \beta_1 = \beta_2 = \frac{\pi}{2} \)이다. 따라서 \[ m_{11} = - N_1 N_2, \quad m_{22} = - N_2 N_1, \quad m_{12} = m_{21} \quad (1-9) \] 을 구한다. 진폭조건은 \( N_1 = N_2 N_s \)가 된다.
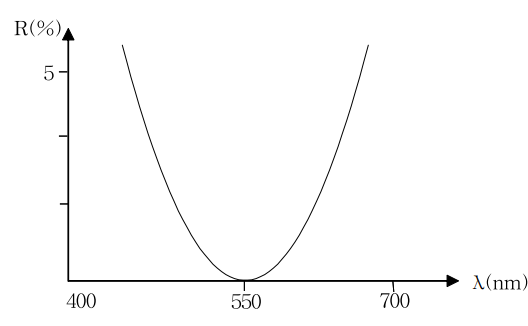
위 그림에 나타냈듯이 V coat는 어떤 특정의 파장 \( \lambda_0 \)에 대해서는 반사율을 거의 0으로 할 수가 있지만, \( \lambda_0 \)이외의 파장에서는 급격히 반사율이 증가한다. 따라서, 광대역ㆍ저 반사율을 기대하는 경우는 다음의 W coat이 좋다.
(B) W coat \( (N_1d_1 = \frac{\lambda_0}{2}, N_2d_2 = \frac{\lambda_0}{4}) \)
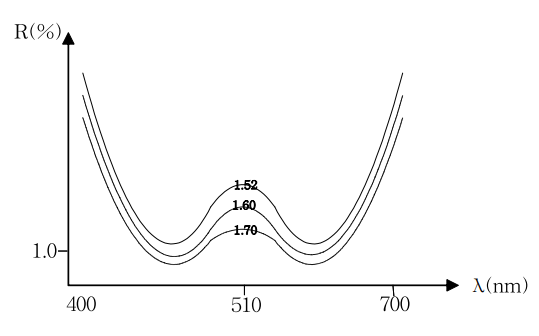
이 무반사 박막은 2개의 파장에서 극소값을 가져 \( \lambda = \lambda_0 \)에서는 극대가 된다. 우선 기준파장 \( \lambda_0 \)에서는 \( \beta_1 = 2\beta_2 \)이므로, \[ m_{11} = m_{22} = 0, \quad m_{12} = i \frac{1}{N_2}, \quad m_{21} = iN_2 \quad (1-10) \] 가 되어 2층막의 특성행렬에 \( N_1 \)의 항이 빠지게 된다.
이것은 단층 무반사 박막의 경우에서 기술된 것처럼, 광학적 박막이 \( \frac{\lambda_0}{2} \) 및 2의 정수배인 것처럼 막은 파장 \( \lambda_0 \)에서는 반사율 및 투과율에 영향을 미치지 않는다는 것이다. 따라서 \( \lambda_0 \)에 있어서 반사율은 제2층의 막두께와 굴절률에 의해 결정된다.
'Optics > Wave optics' 카테고리의 다른 글
| 5. 박막 두께 측정은 어떻게 하는가? (0) | 2023.11.30 |
|---|---|
| 4. 진공에 대해 자세히 알아보자 (1) | 2023.11.29 |
| 2. 단층 무반사 박막을 설계해보자. (0) | 2023.11.28 |
| 1. 진공 증착에 대하여 (0) | 2023.11.28 |



