


아래 그림에서 처럼 굴절률이 작은 매질 내에 있는 평면파면 AB가 굴절률 이 큰 매질과의 경계면 A점에 t = 0시간에 도달한다고 하자.
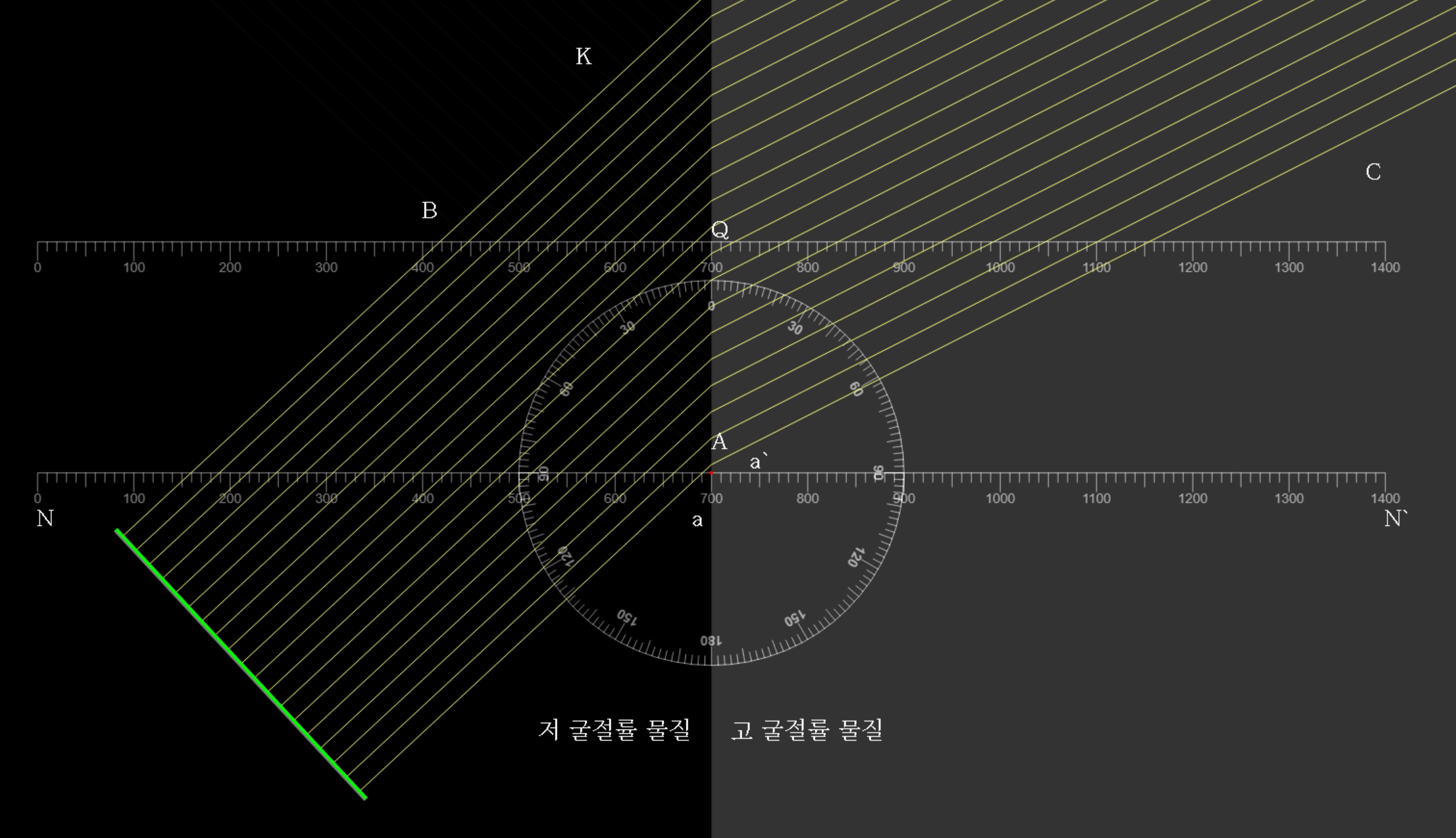
A점은 굴절률이 큰 매질로 들어가는 잔물결들의 새로운 근원점이 된다.
Huygens는 밀도가 큰 매질에서는 잔물결이 더욱 느리게 이동한다고 가정했다.
결과적으로 파면이 B로부터 D로 속도 Va로 굴절률이 작은 매질을 지나는 동안에 잔물결은 굴절률이 큰 매질에서 속도 Vb로 이동하여 반경 AC에까지 확장된다.
B로부터 D까지 가는데 경과되는 시간은 A로부터 C까지 이동하는데 경과되는 시간과 같다.
따라서 각각의 매질에서의 경과 시간들은
\( t = \frac{BD}{Va} = \frac{AC}{Vb} \)
또한 잔물결의 반경은 다음과 같다.
\( AC = \frac{Vb}{Va} \times BD \)
중간점 Q에 대하여 비슷한 구성을 하게 되면 파면이 D에 도달하게 되는 그 순간의 반경은
\( QR = \frac{Vb}{Va} \times KD \)
이다.
Huygens의 원리에 따르면 새로운 파면 CD는 모든 잔물결들에 대한 접선 면이 되고 광선은 파면에 대하여 수직방향으로 진행한다.
굴절에 대하여 Huygens원리를 적용하고 위 그림을 고려하여 Snell의 법칙을 만족하는지 생각해보자. 각 NAR = a:, 보각 BAN은 90―a이고 DAB는 보각과 같아서 a가 된다.
비슷하게, 각 N'AC=a' 이고, CAD는 보각90-a' 이며, 직각삼각형 ACD에서 각 ADC= a'이므로
\( \sin(a) = \frac{BD}{AD} = \frac{Va \times t}{AD} \)
\( \sin(a') = \frac{AC}{AD} = \frac{Vb \times t}{AD} \)
이므로 따라서
\( \frac{\sin(a)}{\sin(a')} = \frac{Va}{Vb} = \text{상수} \)
이다.
상수는 두 매질의 상대 굴절률 Nab와 같다. Huygens의 원리에 따른 광선 진행 및 경로에 대한 구성은 Snell의 법칙을 만족함을 알 수 있고, 굴절 률이 큰 매질에서는 빛의 진행속도가 늦어진다고한 가정이 올바른 가정임을 알 수 있다.
'Optics > Ray optics' 카테고리의 다른 글
| 13. 광학적 경로길이(OPL) (1) | 2023.11.11 |
|---|---|
| 12. 광선 가역성의 원리 (0) | 2023.11.10 |
| 10. Fermat의 최소 시간의 원리: 굴절의 법칙 (0) | 2023.10.24 |
| 9. 평면 거울의 시야 (1) | 2023.10.23 |
| 8. 편향각은 무엇인가? (0) | 2023.10.23 |



