


Pierre de Fermat는 17세기에 프랑스에 살던 수학자인데, "nature is economical"과 같은 견해를 갖고 있었다. 그의 철학의 결과로써 1657년에 다음과 같은 공리를 주장했다.
Femat의 최소 시간의 원리 (Ferma 's PrincipIe of Least Time):
빛은 두 점 사이를 이동할 때 최소시간이 걸리는 경로를 택하여 이동한다.
균일매질(빛의 속도가 일정하게 유지되는)에서 최소시간과 최단경로가 동 일하므로 반사의 법칙을 유도 하는 데에 Hero의 원리가 잘 적용되었던 것처 럼 Fermat의 원리를 사용해서도 반사의 법칙을 유도할 수 있다. 물론 Fermat 의 원리를 사용하면 굴절의 법칙도 유도할 수 있다.
굴절률이 다른 분리된 두 매질 사이의 경계를 가로질러 광선이 진행한다고 생각해 보자. 굴절률이 다른 두 매질 내에서 빛의 속도는 서로 다르게 된다.
아래 그림처럼 A 점을 출발한 광선이 경계의 o 점을 지나 B 점으로 진행한다고 가정해보자. o 점의 위치를 결정하고 입사각과 투과각 사이의 관계를 구해보자.
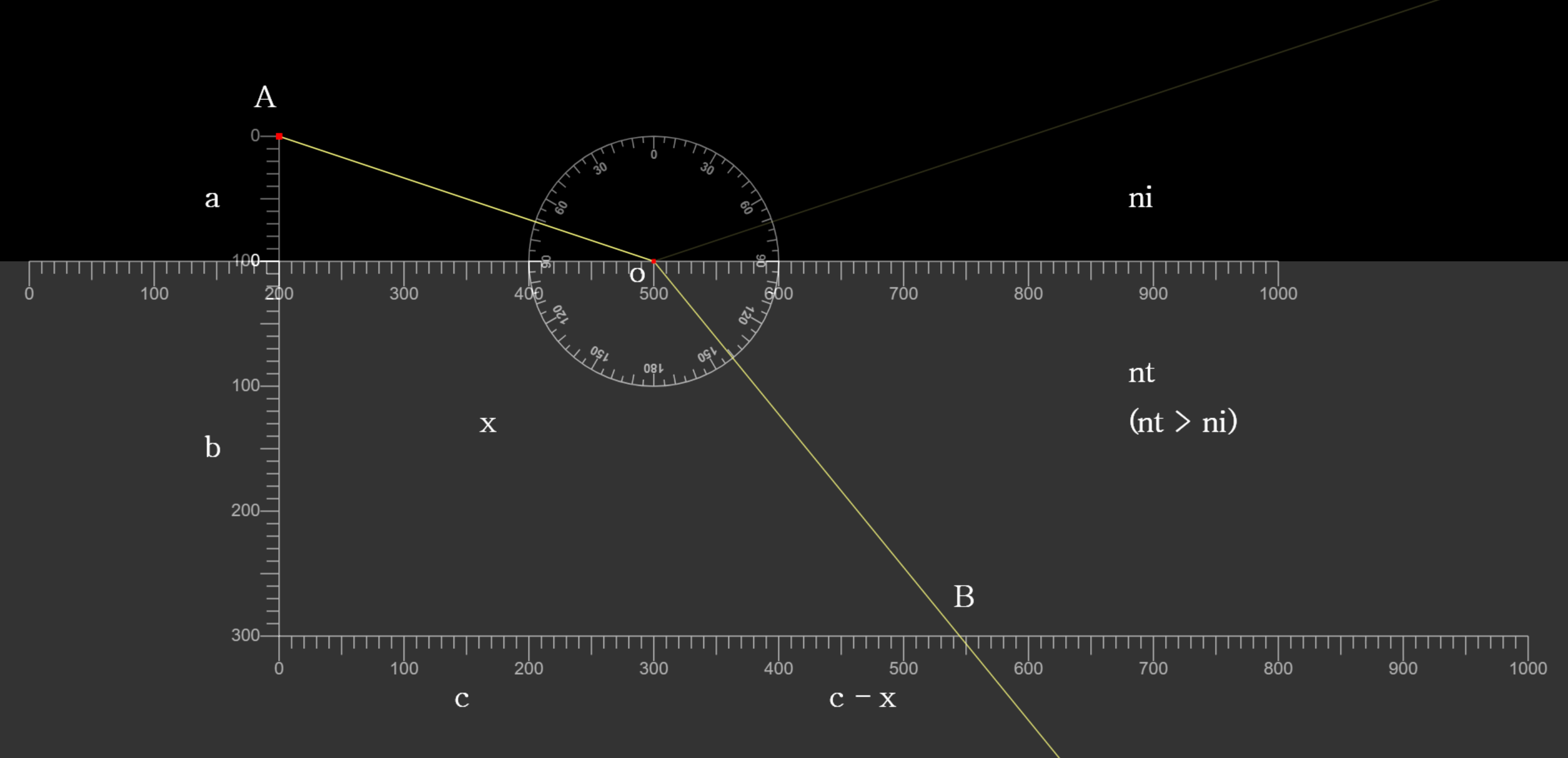
"i ”로 표기된 매질 내에서 빛의 속도는 Vi 이고, "t ”로 표기된 매질 내에서 빛의 속도는 Vt 라 하고 A 점으로부터 B 점으로 이동하는데 리는 전체 시간을 구하면, 이동시간 = 거리/속도 이므로
\[ t = \frac{{d_i}}{{v_i}} + \frac{{d_t}}{{v_t}} \]
\[ t = \frac{{\sqrt{A^2 + x^2}}}{{v_i}} + \frac{{\sqrt{B^2 + (c-x)^2}}}{{v_t}} \]
\[ t(x) = \frac{{\sqrt{A^2 + x^2}}}{{v_i}} + \frac{{\sqrt{B^2 + (c-x)^2}}}{{v_t}} \]
\[ \frac{{dt}}{{dx}} = \frac{{x}}{{v_i \sqrt{A^2 + x^2}}} - \frac{{(c - x)}}{{v_t \sqrt{B^2 + (c-x)^2}}} = 0 \]
\[ \sin(\text{입사각}) = \frac{{x}}{{\sqrt{A^2 + x^2}}}, \quad \sin(\text{굴절각}) = \frac{{c-x}}{{\sqrt{B^2 + (c-x)^2}}} \]
\[ \frac{{\sin(\text{입사각})}}{{v_i}} = \frac{{\sin(\text{굴절각})}}{{v_t}} \]
\[ v_i = \frac{{c}}{{n_i}}, \quad v_t = \frac{{c}}{{n_t}} \]
\[ n_i \sin(\text{입사각}) = n_t \sin(\text{굴절각}) \]
의 관계를 알고 있으므로 이 식들을 대입해 정리하면, 두 매질의 경계에 입 사된 광선과 경계를 투과해 굴절된 광선이 매질의 경계에 수직으로 세운 법 선과 이루는 사이 각들 간에는 Snell의 법칙이라 불리는 디음의 관계가 성립 한다.
굴절의 법칙(SneII의 법칙):
굴절률이 다른 두 매질 사이의 경계를 가로질러 광선이 투과될 때 경계의 양쪽에서 굴절률과 광선각의 Sine값의 곱 은 동일하게 된다.
입사매질의 굴절률이 투과되는 매질의 굴절률보다 작으면 투과된 광선은 매질들의 경계면에 대한 법선 쪽으로 꺾여 지게 되고 반대로 입사 측 매질의 굴절률이 크면 법선에 대하여 멀어지는 쪽으로 꺾이게 된다.
그런데 빛이 실제로 이렇게 행동하는지는 어떻게 알 수 있는가?
ni <nt인 첫 번째 경우를 생각해보자. Snell의 법칙은 sin(입사각)= ntsin(굴절각)/ni가 된다.
또한sin(theta) 의 값은 theta 의 값이 0 으로부터 pi/2 까지 증가함에 따라 단조적으로 증가하는 함수이다.
따라서 (theta)i > (theta)t, (입사각 > 굴절각) 이어야 올바르게 된다.
그런데 위에 주어진 두 그림 중 하나가 옳다고 확신 한다면,
”가역성의 원리 (Principle of Reversibility)”를 사용하여 다른 하나도 옳다고 생각할 수 있다.
'Optics > Ray optics' 카테고리의 다른 글
| 12. 광선 가역성의 원리 (0) | 2023.11.10 |
|---|---|
| 11. Huygens의 원리 (1) | 2023.10.25 |
| 9. 평면 거울의 시야 (1) | 2023.10.23 |
| 8. 편향각은 무엇인가? (0) | 2023.10.23 |
| 7. 두 개의 거울에 의한 광선의 편향 (0) | 2023.10.23 |



