


플라즈마가 전기적으로 준 준성이지만 디바이 길이 보다 작은 길이에서는 전기적인 중성이 약간 벗어날 수 있고 이로 인해 전기장 섭동이 생길 수 있다.
전자 질량이 가볍기 때문에 이러한 전기장 섭동에 전자는 이온 보다 빨리 반응한다.
섭동에 대한 이러한 전자의 반응은 진동으로 나타나는 데 이를 플라즈마 진동이라고 하며,
이때의 진동수를 ‘플라즈마 진동수’ 라고 한다.
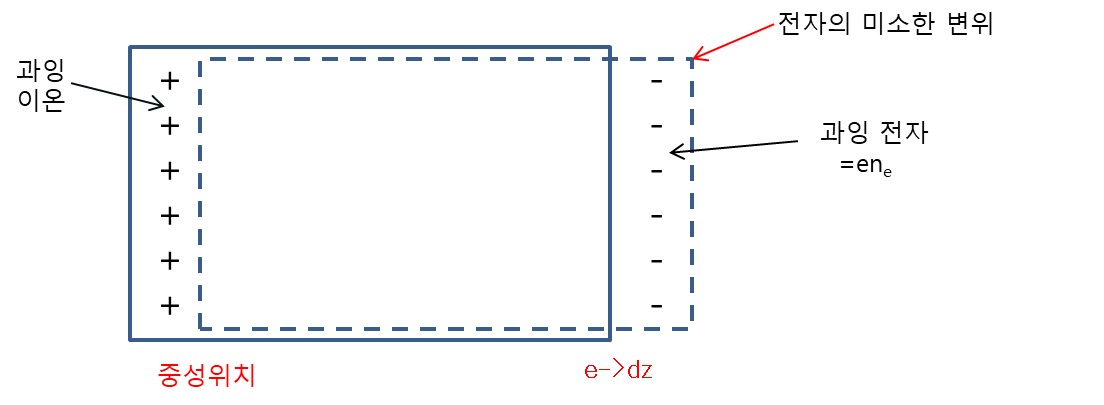
푸아송 방정식:
\( \nabla \cdot \mathbf{E} = -\frac{\rho}{\varepsilon_0} \)
전기장:
\( \frac{dE_z}{dz} = -\frac{e n_e}{\varepsilon_0} \), 따라서 \( E_z = -\frac{e n_e z}{\varepsilon_0} \)
전자에 대한 힘의 방정식:
\( m_e a = -eE_z \)
따라서 \( \frac{d^2 z}{dt^2} = -eE_z = \frac{e^2 n_e z}{\varepsilon_0 m_e} \)
또는 \( \frac{d^2 z}{dt^2} = \omega_p^2 z \)
플라즈마 진동수:
\( \omega_p = \sqrt{\frac{n_e e^2}{\varepsilon_0 m_e}} = 18,000 \sqrt{n_e} \text{ Hz} \)
보통 플라즈마 밀도는 \( 10^{10} \text{ cm}^{-3} \) 에서 \( \omega_p \approx 9 \times 10^8 \text{ Hz} \)
(RF 플라즈마에서 만드는데 사용하는 13.56 MHz 보다 플라즈마 진동수는 훨씬 크다)
플라즈마에서 전자의 열적 운동속도:
\( \frac{1}{2} m_e v_e^2 = \frac{3}{2} kT_e \)
따라서 \( v_e = \sqrt{\frac{2 kT_e}{m_e}} \)
전자가 플라즈마 진동의 주기동안 디바이 길이 정도만을 움직인다.
'Semiconductor > Plasma' 카테고리의 다른 글
| 8. Plasma sheath에 대하여 (1) | 2023.12.09 |
|---|---|
| 7. Plasma 존재 조건에 대하여 (1) | 2023.12.08 |
| 5. Debye 길이(λD)에 대하여 (2) | 2023.12.06 |
| 4. Plasma 변수에 대하여 (0) | 2023.12.05 |
| 3. Plasma의 특성 및 종류 (0) | 2023.12.03 |



