

30. 측 배율 또는 횡 배율Optics/Ray optics2023. 11. 25. 14:38
Table of Contents
반응형

축 위에 있는 물체 점 M과 상점 M'는 공액점이다.
빛의 가역성은 물체 점과 상점은 교환할 수 있음을 의미하며 서로에 대하여 공액인 상태를 유지 한다.
더욱이, M과 M'과 놓여 있는 광축에 수직인 횡 평면들은 서로 공액 관계에 있는 물체 면과 상면이다.
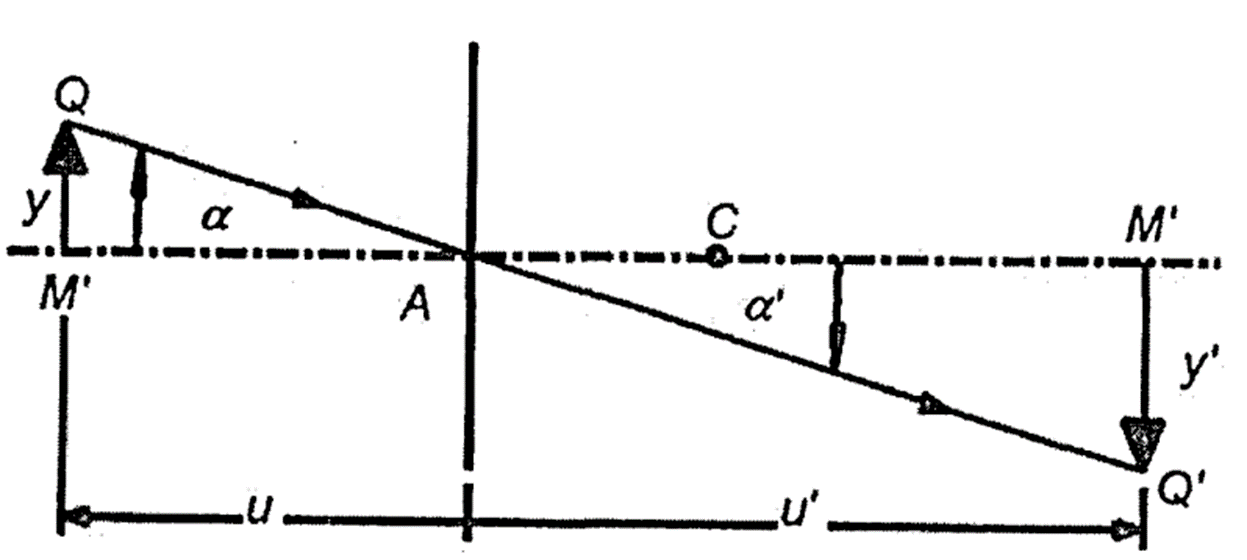
물체 면에 있는 비축 근축 점 Q 는 상면 에 상점 Q' 를 만들게 된다.
물체의 크기 y=MQ이고 상의 크기는 y'= M'Q”이다.
측 배율(Lateral magnification) Y는 물체의 크기에 대한 상 크기의 비율이다.
\[ Y = \frac{y'}{y} \]
구 굴절면에 의해 만들어진 측 배율에 대한 식은 Snell의 법칙의 근축 형으로부터
\[ \frac{\sin \alpha'}{\sin \alpha} = \frac{\alpha'}{\alpha} = \frac{n}{n'} \]
근축 각들은 그림 참고하여 다시 쓰면, \( \alpha = \frac{y}{u} \) 그리고 \( \alpha' = \frac{y'}{u'} \) 이다. (Radians)
따라서 \( \frac{\alpha'}{\alpha} = \frac{y'}{y} \cdot \frac{u'}{u} = \frac{n}{n'} \) 이므로, 측 배율 Y는
\[ Y = \frac{y'}{y} = \frac{n}{n'} \cdot \frac{u'}{u} \]
반응형
'Optics > Ray optics' 카테고리의 다른 글
| 32. Newtonian 방정식 (1) (2) | 2023.11.26 |
|---|---|
| 31. 평면 굴절면에서 상 방정식 (1) | 2023.11.25 |
| 29. 초점과 초점거리 (1) | 2023.11.25 |
| 28. 근축 상 방정식 (0) | 2023.11.25 |
| 27. 구면 경계면에서의 굴절 (1) | 2023.11.24 |



