3. 푸리에 변환, 그 뜻과 개념

 

 

FDTD는 푸리에 변환을 통해서 TIme 및 Frequency Domain을 계산한다.

푸리에 변환이 뭔지 간단히 알아보자.

 

푸리에변환, 푸리에급수를 발전시킨 것이다.

푸리에변환은 푸리에급수와 관계가 있다.

푸리에 급수가 무엇이었던가?
주기가 있는 복잡한 파동을 sin, cos 처럼 단순한 파동들의 합으로 표현하는 것이었다.
각 파동들의 계수를 알아내는 것이 푸리에계수였다. 

 

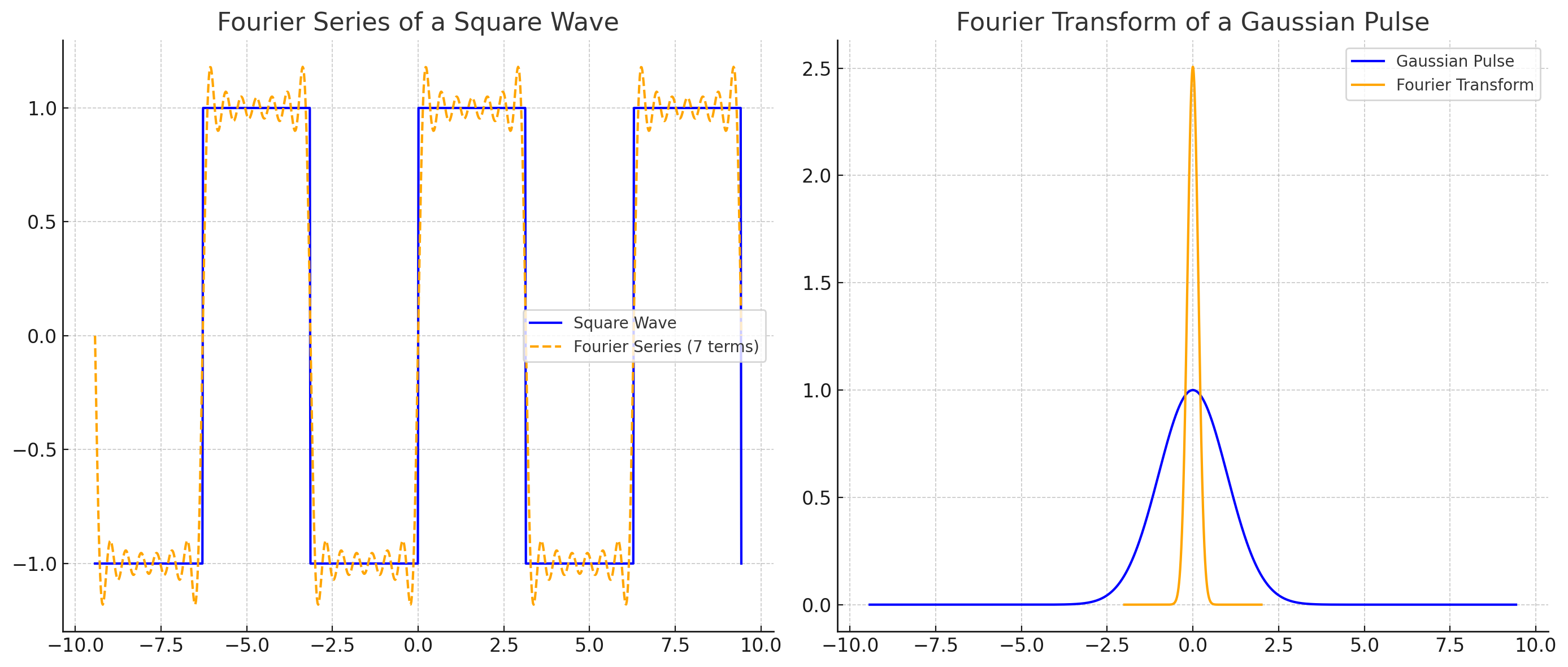
Fourier Series

푸리에 급수는 주기 함수를 사인과 코사인 함수의 합으로 나타난다.

\(f(t)\)가 주기 \( T \)인 주기 함수인 경우, 푸리에 급수 전개는 다음과 같이 주어진다:

• \( a_0 = \frac{1}{T} \int_0^T f(t) \, dt \)
• \( a_n = \frac{2}{T} \int_0^T f(t) \cos\left(\frac{2\pi nt}{T}\right) \, dt \)
• \( b_n = \frac{2}{T} \int_0^T f(t) \sin\left(\frac{2\pi nt}{T}\right) \, dt \)

계수 \( a_n \) 및 \( b_n \)은 푸리에 계수다!

 

Fourier Transform

 

푸리에변환, 주기가 없는 파동을 단순 파동들의 합으로 만드는것!

 

푸리에급수는 주기가 있는 파동을 대상으로 했다.
복잡하지만 일정한 주기를 갖고 반복되는 파동을 다뤘다.
주기가 없는 파동을 다루지 못했다.

 

푸리에변환은, 주기가 없는 파동을 다룬다.
그런 파동을 단순한 파동들의 합으로 나타낸다.
훨씬 더 포괄적이다.

 

푸리에 변환은 모든 주파수의 사인 곡선의 합으로 함수를 나타낸다.

함수 \( f(t) \)의 푸리에 변환 \( F(\omega) \)은 다음과 같이 주어진다.:

\[ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} \, dt \]

여기서 \( \omega \)는 각 주파수.

 

푸리에변환, 주기를 무한대로 본다.

 

푸리에 변환의 맥락에서 비주기 함수는 "무한 주기"를 갖는 것으로 볼 수 있다.

푸리에급수는 주기 T가 주어져 있었다.
그러나 푸리에변환이 다루고자 하는 파동에는 주기가 존재하지 않는다.
그래서 주기 T를 무한대로 본다.

 

주기를 무한대로 한다고 해서, 무한대 시간 관찰하지는 않는다.
그렇게 할 수도 없다.
그래서 일정 시간인 Δt 동안의 파동을 대상으로 한다.

즉, 푸리에 변환은 무한 신호를 다루지만 실제로는 유한한 시간 \( \Delta t \) 동안만 신호를 관찰할 수 있다.

이 관찰 기간에는 주파수 영역에서 몇 가지 제한 사항과 불확실성이 발생한다.

당연히 부분을 통해서 전체의 특징을 파악해가기에 푸리에변환에는 불확정성이 존재하게 된다.

Uncertainty Principle

푸리에 변환의 맥락에서 불확실성 원리는 신호의 시간 특성 \( \Delta t \)를 결정할 수 있는 정밀도와 신호의 주파수 특성 \( \Delta f \)를 결정할 수 있는 정밀도와 연관된다. 이 관계는 다음과 같이 표현된다:

 

\[ \Delta t \cdot \Delta f \geq \frac{1}{2\pi} \]

 

이 원리는 입자의 위치와 운동량의 불확실성의 곱이 아래에서 경계가 되는 양자역학에서 하이젠베르크의 불확실성 원리를 반영하는 것 이다.

푸리에 영역의 불확실성 원리는 시간과 주파수 특성에 대한 정확한 정보를 동시에 가질 수 없음을 나타낸다.

신호의 시간(small \( \Delta t \))을 찾으려고 하면 주파수 (large \( \Delta f \))에 불확실성이 발생하고, 그 반대의 경우도 마찬가지이기 떄문이다.