2. FDTD Method, 유한 차분 시간 영역법

 

Maxwell's equations - Wikipedia

Finite-difference time-domain method - Wikipedia

Numerical analysis - Wikipedia

 

수치해석이란 결국 사람 손으로 풀지 못하는 것을 컴퓨터가 대신 풀어주는 것입니다.

구할 수 있는 결과는 매우 다양하다. 그러나 그중 대부분은 미분방정식의 해를 구하는 것에 집중합니다.

많은 물리적인 상황은 미분방정식의 형태로 표현되고, 상황이 복잡해질수록, 우리가 원하는 해를 구하는 것 또한 점점 어려워지고 있습니다. 이렇게 해를 손으로 구하는 것이 어려워지면서, 이러한 미분방정식을 수치적으로 풀기 위한 많은 방법들이 등장하였습니다.

 

미분 방정식

수치적으로 미분 방정식을 푼다는 것은 주어진 미분 방정식의 근사해를 찾는다는 것을 의미한다. 이 때는 다음과 같은 전제 조건이 필요하다. 수치 해석적인 방법으로 미분 방정식을 푸는 것에는 다음과 같은 것들이 있습니다.

오일러 방법(Euler's Methods)
룽게-쿠타 방법(Runge-Kutta Methods)

편미분 방정식

상위의 미분 방정식과 비슷한 원리이지만, 차원이 더 커지므로 다른 방식의 수치적 방법을 이용해야 풀 수 있다. 아래에는 두 개의 수치적 방법이 있습니다.

유한차분법 (FDM : Finite Difference Method)
유한요소법 (FEM : Finite Element Method)

 

이번 포스팅에서는 대표적인 편미분방정식 중 하나인 맥스웰 방정식을 수치해석하는 방법 중 하나인 FDTD(Finite Difference Time Domain) 방식에 대해서 설명하려 합니다.

 

Maxwell's Equations

맥스웰 방정식은 전자기학 연구의 기반이 됩니다. 전기장과 자기장이 상호 작용하고 진화하는 방식을 요약합니다. 소스가 없는 영역에서는 다음과 같이 나타납니다:

 

• \( \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} \)
• \( \nabla \times \mathbf{H} = \frac{\partial \mathbf{D}}{\partial t} \)

Discretization

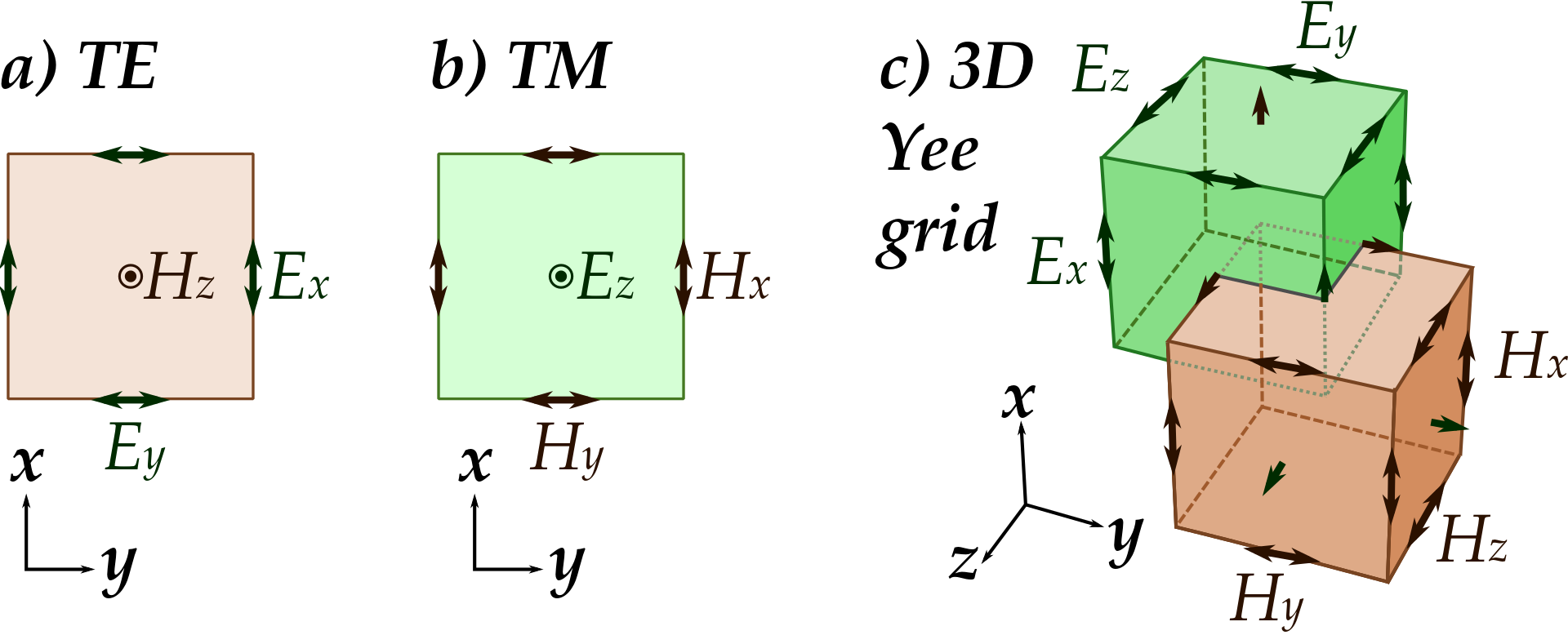
맥스웰 방정식의 시간과 공간의 연속체는 FDTD에서 불연속적인 단계로 대체되어 무한한 가능성에서 유한한 계산으로 영역이 전환됩니다.

 

• Temporal Discretization: FDTD 방법은 도약 방식입니다. 전기장은 다음과 같이 불연속적인 풀타임 단계로 계산됩니다. \( n\Delta t \), 반면 자기장은 다음과 같이 반정수 시간 단계로 계산됩니다.  \( (n+\frac{1}{2})\Delta t \). 이러한 엇갈린 시차 방법론을 통해 시뮬레이션의 안정성과 계산 정확도를 모두 보장하게 됩니다.
• Spatial Discretization with the Yee Cell: 1966년 케인 이가 제안한 이 셀 또는 격자는 전기장 및 자기장 구성 요소를 공간적으로 엇갈리게 배치하여 정확도를 높이는 격자 구조입니다. 예를 들어 \( E_x \)가 공간 위치 \( (i,j,k) \)에서 계산되는 경우, 자기장 \( H_y \) 및 \( H_z \)는 반 공간 떨어진 곳에서 알 수 있습니다.

 

Update Equations in FDTD

업데이트 방정식은 맥스웰의 컬 방정식에서 연속 도함수를 이산 차분으로 대체하여 파생됩니다. 여기서는 \( E_x \)에 대한 업데이트 방정식에 초점을 맞춰 자세히 설명하겠습니다.

 

\( E_x \) Update:

x-성분에서 \( E \)의 컬은 다음과 같습니다:

\[ (\nabla \times \mathbf{E})_x = \frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z} \]

이는 중심 차이를 사용하여 다음과 같이 이산화할 수 있습니다:

\[ (\nabla \times \mathbf{E})_x \approx \frac{E_z(i,j+1,k) - E_z(i,j,k)}{\Delta y} - \frac{E_y(i,j,k+1) - E_y(i,j,k)}{\Delta z} \]

이제 패러데이의 법칙 \( \nabla \times E = -\frac{\partial B}{\partial t} \)를 사용하고 \( B = \mu H \)에 맞추면 다음과 같이 됩니다:

\[ -\frac{\partial H_x}{\partial t} = \frac{E_z(i,j+1,k) - E_z(i,j,k)}{\Delta y} - \frac{E_y(i,j,k+1) - E_y(i,j,k)}{\Delta z} \]

이를 재배열하여 \( H_x \)에 대한 업데이트 방정식을 구할 수 있게됩니다.

\[ H_x(i,j,k)^{n+1/2} = H_x(i,j,k)^{n-1/2} + \frac{\mu \Delta t}{\Delta y} (E_z(i,j+1,k)^n - E_z(i,j,k)^n) - \frac{\mu \Delta t}{\Delta z} (E_y(i,j,k+1)^n - E_y(i,j,k)^n) \]

이는 자기장이 반정수 시간 단계로 업데이트되고 전기장이 정수 시간 단계로 업데이트되는 도약 방식이라고 하죠. 다른 필드 구성 요소 \( E_y, E_z, H_y \) 및 \( H_z \)도 비슷한 방식으로 유도할 수 있겠습니다.

 

결과적으로 불연속형 환경으로 구성된 다음 단계는 전기장과 자기장을 정수 시간만큼 시간 배열이 붕괴될 때까지 업데이트하는 것으로, 이 과정은 아래의 최종적인 FDTD 업데이트 방정식을 사용하여 진행됩니다.

 

Electric Field Updates: 패러데이의 법칙을 이산화 하면 전기장에 대한 업데이트 방정식은 다음과 같습니다.:

• \( E_x^{n+1}(i,j,k) = E_x^n(i,j,k) + \frac{\Delta t}{\epsilon \Delta y} \left( H_z^{n+1/2}(i,j,k) - H_z^{n+1/2}(i,j-1,k) \right) - \frac{\Delta t}{\epsilon \Delta z} \left( H_y^{n+1/2}(i,j,k) - H_y^{n+1/2}(i,j,k-1) \right) \)

 

... 그리고 \( E_y \) 및 \( E_z \)에 대해서도 유사하게 계산합니다.

 

 

Magnetic Field Updates: 이하 동일하게 암페어의 법칙을 이산화 하면 자기장에 대한 업데이트 방정식은 아래와 같죠:

• \( H_x^{n+1/2}(i,j,k) = H_x^n(i,j,k) - \frac{\Delta t}{\mu \Delta y} \left( E_z^{n+1}(i,j,k) - E_z^n(i,j-1,k) \right) + \frac{\Delta t}{\mu \Delta z} \left( E_y^{n+1}(i,j,k) - E_y^n(i,j,k-1) \right) \)

 

... 그리고 \( H_y \) 및 \( H_z \)에 대해서도 유사하게 계산됩니다.