

2. Optimum Launching Condition for Hollow FiberOptics/Miscellaneous2023. 12. 1. 23:51
Table of Contents
반응형

Solid-State Lasers for Materials Processing
Laser Beam의 Fiber Coupling 관련 포스팅입니다.
회사에서 레이저 빔 사이즈 구하는 일이 있어서
일하는 김에 작성합니다 ^^,,
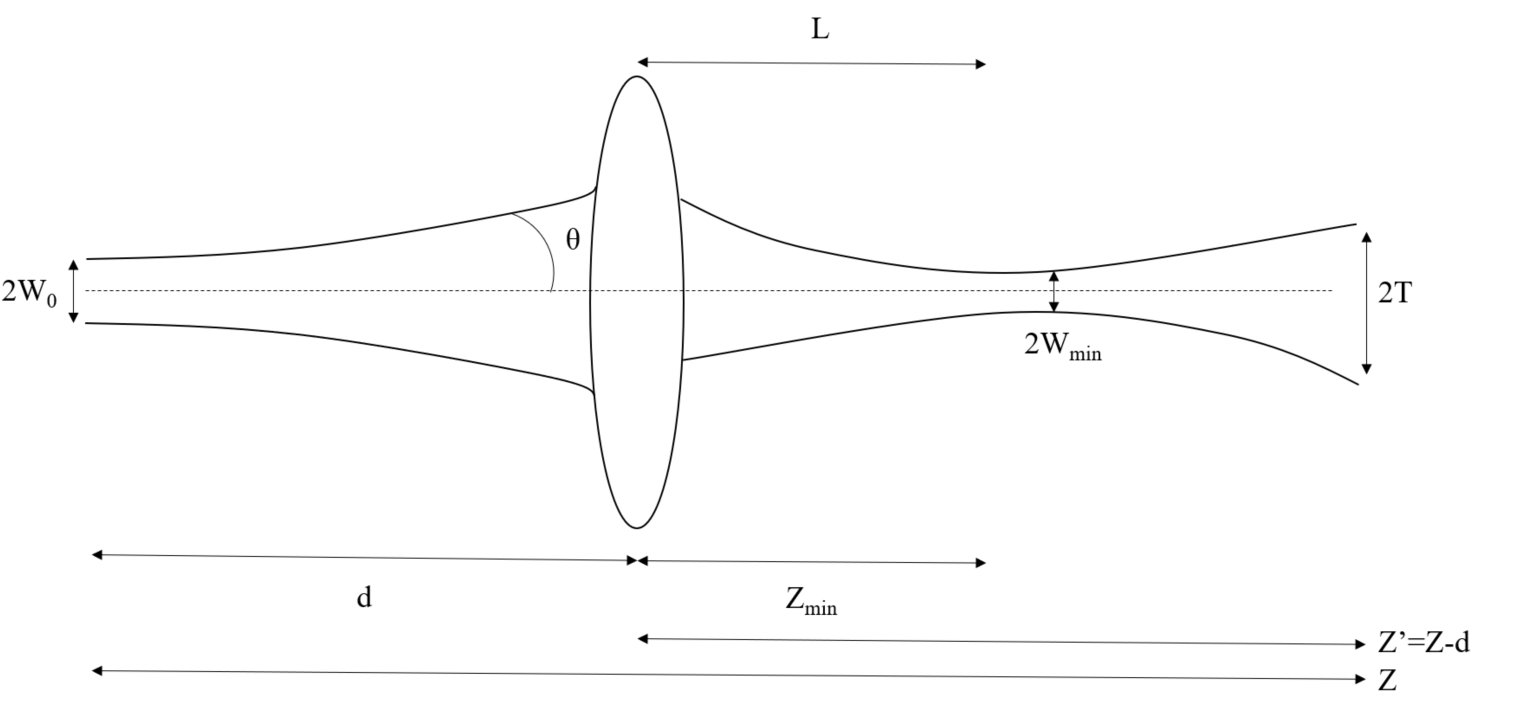
Basic: 렌즈를 이용한 레이저빔 집속을 설명하는 수식:
\[ w_f = \frac{\lambda \times f}{\pi \times w_0} \]
- \( w_f \): 초점에서의 빔 직경
- \( w_0 \): 입사빔의 직경
- \( \lambda \): 레이저 파장
- \( f \): 렌즈 초점거리
이를 응용해서...
- Wavelength: \( \lambda \)
- Beam waist: \( w \)
- Half divergence angle at beam waist: \( \theta_0 = \frac{\pi \theta}{2 w_0} \)
- Minimum waist radius: \( w_{min} \)
- Length: \( L \)
- Focal Length: \( f \)
- Minimum waist diameter: \( 2w_{min} \)
- Divergence angle: \( \theta \)
- Minimum Rayleigh distance: \( Z_{min} \)
- Period: \( 2T \)
- Corrected distance: \( z' = z - d \)
와 같을때 다음과 같은 식으로 정리할 수 있다.
- Beam radius for \( Z \leq d \): \( w = w_0 \sqrt{1 + \left(\frac{\pi w_0}{\lambda z}\right)^2} \)
- Beam radius for \( Z \geq d \): \( w = w_0 \sqrt{\left(\frac{(z' - 1)}{f}\right)^2 + \left(\frac{\pi w_0}{f\lambda}\right)^2} \)
- Minimum beam radius: \( w_{min} = f w_0 \sqrt{(d - f)^2 + \left(\frac{\pi w_0}{\lambda}\right)^2} \)= \( 1 = \sqrt{\left(\frac{\pi \lambda}{2(1 - d/f)^2 \theta^2} + (f\theta)^2\right)} \)
- Minimum Rayleigh distance: \( Z_{min} = \frac{((d - f)f^2)}{((d - f)^2 + \left(\frac{\pi w_0}{\lambda}\right)^2)} + f \)
\( L = Z_{min} \) and \( W_{min} \approx 0.6 \times T \).
반응형
'Optics > Miscellaneous' 카테고리의 다른 글
| 6. What is light? (0) | 2024.03.19 |
|---|---|
| 5. Laser Spot Size Calculator, 레이저 초점 크기 계산기 (1) | 2023.12.26 |
| 4. 대기에서 빛의 산란, 왜 하늘은 파란색인가? (1) | 2023.12.23 |
| 3. Huygens-Fresnel principle, Remind Diffraction (2) | 2023.12.05 |
| 1. 물체 및 상거리, S 와 S` 구하기 (0) | 2023.10.05 |



