


이전 포스팅에 이어 계속 하려합니다. 쭉 언급한 내용이지만 중요하게 짚고 넘어가야 할 점은 EUV 빛은 흡수가 잘되기에 투과가 되지않습니다. 그러므로 EUV 광학계는 투과 광학계 대신 반사 광학게를 사용하여 빛을 웨이퍼에 전달하는 시스템을 가지고 있습니다! 그러기에 EUVL에 사용되는 광학 시스템은 복잡하고 복잡하게 설계되어 반사 이미징 시스템 설계의 지속적인 혁신과 발전이 필요합니다.
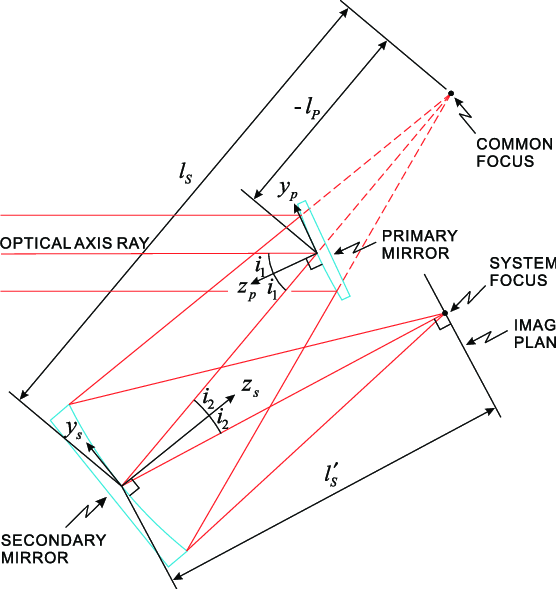
이전의 포스팅에서도 설명하였듯, EUVL 광학 시스템의 발전은 Schwarzschild 광학의 구현으로 시작되었습니다. 다시한번 간략하게 설명드리자면 독일의 물리학자이자 천문학자인 Karl Schwarzschild의 이름을 딴 Schwarzschild 광학은 두 개의 거울을 활용하는 광학 시스템입니다. 이 구성은 EUVL의 역사와 미래에 직접적인 영향을 미쳤죠. Schwarzschild 광학 시스템의 특징 중 하나는 하나의 축에서 수차 없는 이미지를 생성하는 기능입니다. 수차를 제거한다는것은 광학계에서 엄청 난 이점을 가진다는 것입니다. 이 특성을 얼마나 큰 장점인지 이해하려면 광학 수차 현상을 먼저 알아야겠죠?
광학에서 수차는 광학 시스템에서 빛의 편차를 말하며 이미지가 흐려지거나 왜곡되는 현상을 말합니다. 이러한 수차는 구면 수차, 색채 수차, 코마 수차, 비점수차, 왜곡 또는 상면 만곡일 수 있습니다. 또한 각각은 수차는 이미지 형성 과정에서 서로 다른 특성을 보입니다. 아래의 링크를 통해 수차의 간단한 특성을 살펴보실 수 있습니다! 수차가 발생이되면 초점의 이미지는 수차의 종류에 따라 다르지만 결과적으로 얼룩이 묻은것처럼 이미지화됩니다. 이 왜곡은 최종 이미지의 선명도를 감소시켜 반도체 제조 또는 천체 이미징과 같이 높은 정밀도를 요구하는 애플리케이션에 적합하지 않게 만들기 때문에 반드시 해결해야하는 문제입니다.

수차에 대해 정말 자세히 설명된 웹사이트가 있어 아래에 소개드립니다.
혹시 관심있으시면 꼭 찾아보셔요! (저는 자이델과 제르니케가 싫습니다. ^^)
Comparison of Optical Aberrations
www.edmundoptics.co.kr
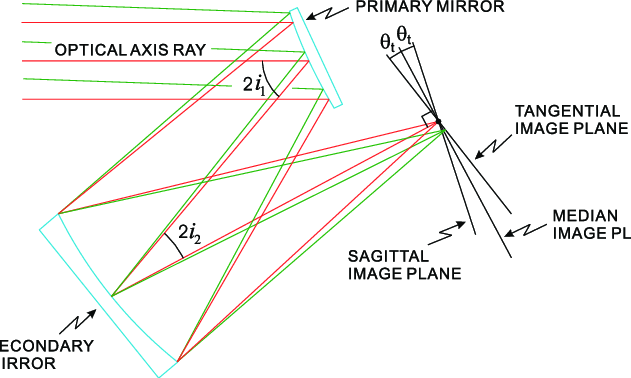
근데 Schwarzschild 광학 시스템을 이용한다면 구면수차를 (물체 점에서 나온 광선이 렌즈나 거울을 통과한 후 한 점에 모이지 않는 수차의 일종)확실하게 제거할 수 있어 이점을 가집니다. 이제 이러한 이점을 가진 광학 시스템이 반도체 제조에 있어 더 큰 특장점을 가지게 되도록 어떻게 변화 했는지 알아봅시다.
Schwarzschild 시스템의 구형 설계는 원래 시스템의 한계를 해결하기 위해 제안된 여러 변형과 함께 발전했습니다. 하지만 초기 실험은 상술한 구형 표면을 가진 슈바르츠실트 광학을 사용했지만, 이러한 설계는 EUVL에 적합하지 않았습니다. 최초의 실용적인 디자인은 텔레센트릭 디자인의 두 개의 비구면 거울을 사용한 Kinoshita으로부터 왔습니다. 이 시스템은 고리 모양의 FOV를 가지고 있었습니다. 이후 개발된 4-미러 및 6-미러 시스템은 후면 간극 개선 및 수차 보정 개선과 같은 이점을 제공했습니다. 또한 단순히 미러를 늘린 것 만이 아니라 Off-axis 시스템을 적용해서 노광 영역를 확대에 기여했죠. EUVL의 맥락에서 필드 크기는 매우 중요합니다. 필드 크기가 클수록 한 번의 작업으로 광원에 노출될 수 있는 실리콘 웨이퍼의 면적이 넓어져 리소그래피 공정의 효율성과 속도를 높일 수 있기 때문이죠. 웨이퍼(집적 회로가 인쇄되는 기판)를 이동하기 위한 스캐닝 스테이지와 축외 위치에서 수차가 거의 없도록 광학 장치를 설계하기 위해 레이 트레이싱(Ray-tracing)이 얼마나 이루어졌을지 감히 상상하지 못할 것 같습니다.
'Semiconductor > EUV lithography' 카테고리의 다른 글
| 6. EUV 개발 역사 (6) - 비구면 거울 측정 (2) | 2023.10.03 |
|---|---|
| 5. EUV 개발 역사 (5) - 비구면 거울의 서막 (6) | 2023.10.02 |
| 4. EUV 개발 역사 (4) - 광학계 거울 구성 (7) | 2023.10.01 |
| 2. EUV 개발 역사 (2) - 광학계의 발전 과정 (0) | 2023.09.29 |
| 1. EUV 개발 역사 (1) - 리소그래피의 발전 과정 (0) | 2023.09.28 |



